Chapter 13. Practical learning research at scale

Kenneth R. Koedinger

Carnegie Mellon University

Many decades of attempts to use science to improve education has produced limited success. Greater success will be achieved through research done within the practice of education. The suggestion is not to simply apply learning science to practice but rather to produce new learning science in real educational settings. The increasing use of technology in schools, from intelligent tutoring systems to mixed-reality games, makes it feasible like never before to engage in systematic experimental investigations of principles of learning and techniques for best supporting it. Systematic investigation is necessary because it is now clear that among the trillions of different ways to support learning, existing science tells us too little about what works best. We present the Knowledge Learning Instruction (KLI) framework to provide guidance on how to do learning research in practice in a way that is driven by data, advances new learning theory and provides a roadmap to better education.

Education is fundamentally important to the world’s progress. Science and technology are increasingly creating new learning opportunities that are yielding better outcomes, better instruction and better data-driven decisions. Progress in applying learning science comes with some bad news, good news and even better news. The bad news is that there is a large implementation gap between what we know in the learning sciences and what is being used in educational practice (Chapter 18, by Means, Cheng and Harris). The good news is that a considerable amount of progress has been made in developing a science of learning that is relevant to improving educational practice. For example, recent evidence demonstrates that applying learning science in technology-enabled courses can double learning outcomes. Other chapters in this book provide further examples (Chapter 8, by Forbus and Uttal; Chapter 12, by Klahr and Siler; Chapter 14, by Rose, Clarke and Resnick). The even better news is that there remains a lot unknown about how human learning works and how it can be optimised. Thus, as new insights accumulate about how learning works and how it may be optimised, it may be possible to not only double the current rate at which people learn, but perhaps make it five or ten times more effective or efficient.

One of the reasons for the implementation gap noted above is that often education stakeholders, from parents and teachers to school administrators and policy makers, do not believe what the science is telling us. Some scepticism is warranted, but a fundamental reason for undue scepticism is that stakeholders are driven by their own intuitions about learning and these intuitions are based on limited information. How learning works in our human brains is not directly visible after all. We often experience illusions of learning both in observing ourselves and others. What learning scientists do is use data about what students know and how it changes over time to make inferences about when and how learning is working. To unlock the many remaining mysteries of human learning and turn insights into radically better education, we need both scientists and educational practitioners to work together to engage in scientific analysis of bigger and better learning data.

We need a practical learning science endeavour that operates at scale in real educational settings and we need it to address two substantial challenges. The first challenge is in developing deep insight into the educational subject matter we teach, whether it is reading, maths, collaboration skills or learning skills. Turns out, you cannot just ask experts what they know. Experts are only consciously aware of about 30% of what they know, that is, they do not know what they know (Clark et al., 2007[1]). The second challenge is in figuring what are the best ways to teach. When one considers the combinations of the many recommendations that learning science literature provides, it becomes evident that the design space of alternative ways to teach and support learning is immense (Koedinger, Booth and Klahr, 2013[2]). Further extending this challenge, there is accumulating evidence that instructional designs that work well in one context (e.g. with a particular student population or course content) do not work in other contexts (Koedinger, Corbett and Perfetti, 2012[3]).

We raise these challenges not to criticise the current state of learning science and its practical application, but rather to suggest that there is great opportunity for the application of better learning science and technology to make revolutionary improvements upon the current state of educational practice. Educational technology is not only increasing spreading access to high-quality and sometimes personalised instruction, but it also has the great potential to provide the data we need to address these grand challenges and advance a practical learning science that can revolutionise education (Singer and Bonvillian, 2013[4]). Student learning could be many times more effective than it is today!

Practical learning science challenges

Learning is a bit like magic – filled with lots of illusions as it occurs, in our brains, behind a curtain of limited self-conscious reflection. Both students and instructors generally think they know they or their students are learning. However, evaluations of students’ judgement of learning have found quite low correlations between students estimates of learning and actual test scores (Eva et al., 2004[5]). One reason learners fail to accurately predict their own learning is that they have insufficient mental resources to learn and monitor their own learning (Moos and Azevedo, 2008[6]). As non-experts, they do not know what to monitor: How can they compare their emerging ideas and skills with correct ideas and behaviours when they do not yet have the expertise to know what is correct? Learners experience further illusions of learning when they base their judgements on what they like – what students actually learn from a course has been shown to be poorly correlated with how much a student likes a course (Sitzmann et al., 2008[7]). For similar reasons, instructors can be fooled by observing students’ facial expressions. Many seek happy faces and avoid looks of confusion. But student struggle and confusion can often aid long-term learning outcomes as international research (Bjork, 1994[8]; Kapur and Rummel, 2012[9]).

Public dialogue argues between learning basics vs. understanding, as though there are two dimensions to learning. Learning science research, on the other hand, elaborates more dimensions (Clark and Mayer, 2012[10]; Pashler et al., 2007[11]) and many contradictions. For example, many studies indicate that spaced practice is better than massed practice for long-term retention (Pashler et al., 2007[11]) yet, under certain circumstances massed practice is better (Pavlik and Anderson, 2008[12]). Direct instruction is sometimes better than discovery learning (Klahr and Nigam, 2004[13]) but in other contexts active learning is emphasised (Wieman, 2014[14]). Often which type of instruction is more beneficial has to do with either reducing students’ cognitive load by offering more instructional assistance or creating desirable difficulties by reducing instructional assistance for students to construct their own knowledge (Koedinger and Aleven, 2007[15]).

The instructional design space for learning is roughly organised along the two dimensions argued in the education wars (i.e. basics vs. understanding or more assistance vs. more challenge). Koedinger, Booth and Klahr (2013[2]), articulated 30 dimensions with numerous combinations (e.g. study worked examples or do practice problems or a mixture of both, more concrete or more abstract problems, more immediate or more delayed feedback, etc.) illustrating the vastness of the design space and the wide spectrum of possibilities beyond the two condition comparison (see Figure 13.1). There are over 200 trillion different ways to design instruction!

Figure 13.1. Illustration of the enormity of instructional design space

Scaled applications of learning by doing with feedback

Approximately a half million students per year are using Mathematics Cognitive Tutors in K-12 classrooms for about 80 minutes a week (roughly two class periods). A recent big study (~149 schools) by RAND Corporation showed a doubling of student achievement in a Cognitive Tutor Algebra course over the school year as compared to a traditional algebra course (Pane et al., 2014[16]). Note that these results are a consequence of using the text and teacher professional development materials that are part of the course, not just the technology.

In addition, college-level online courses such as the Open Learning Initiative (OLI) at CMU have incorporated the learn-by-doing approach and have reached some fairly good scale. About 30 college introductory courses are in use in approximately 1 000 colleges. These kinds of educational technologies that are widely used, not just cognitive tutors and OLI courses but also language learning online courses and some educational games provide an opportunity to do basic research in the context of functioning courses. One striking demonstration of improving learning through data-driven design of a course was a study that compared a traditional introductory statistics course taught over a full semester with a blended version of the course that used OLI materials, had a classroom instructor and was taught in half a semester (Lovett, Meyer and Thille, 2008[17]). The blended course taught in half a semester had an 18% pre to post gain on a standardised test vs. a 3% gain for the traditional course.

In other words, large amounts of data generated by widespread use of educational technologies creates a cyberinfrastructure for doing science in practice. Researchers like educational psychologists and cognitive psychologists can get out of the laboratory and run studies in real classrooms. Collaborations can be fostered with diverse groups of professionals across a global front inspiring creative investigations and experimentation.

The Knowledge Learning Instruction (KLI) framework

Lessons learned from the hundreds of cross-domain in vivo experiments were critical in the development of theory for making sense of the contradictory research results in the instructional design space.

The Knowledge Learning Instruction (KLI) framework (Koedinger, Corbett and Perfetti, 2012[3]) provides means to understand the inconsistencies and competing recommendations across the different disciplines of the learning sciences. Inconsistent results and competing recommendations are not a simple consequence of limited data or poor research designs but can often be explained by noting differences in the nature of the knowledge that is to be acquired across different research studies.

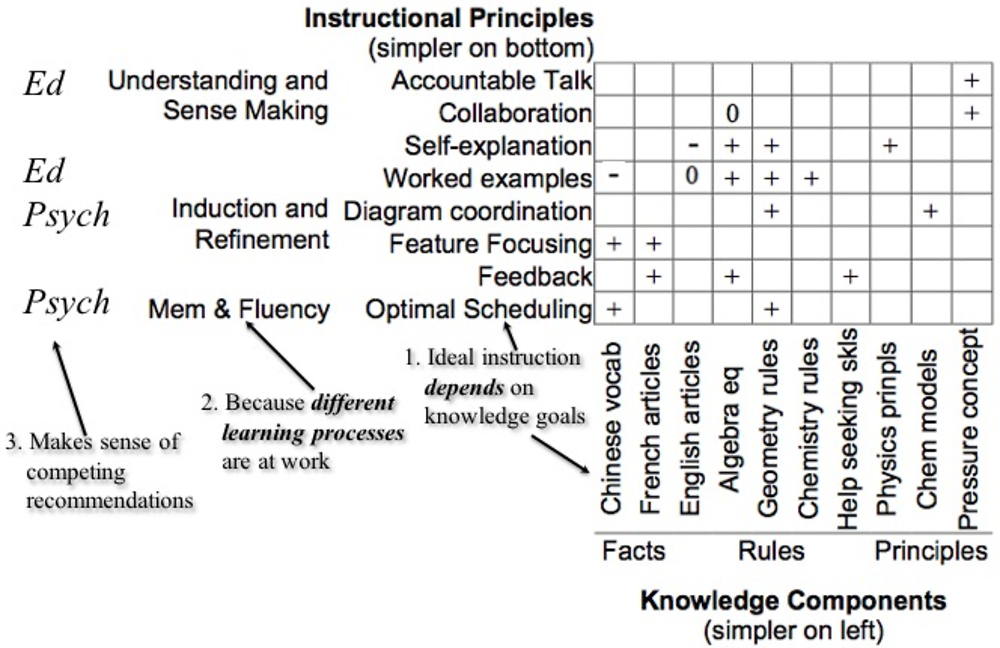
The KLI framework maintains that the success of different instructional principles across domains is dependent upon knowledge goals (see Figure 13.2). Furthermore, understanding the learning for these different kinds of knowledge goals will help determine what instructional principles are most effective (see Figure 13.2). For example, if your goal is learning Chinese vocabulary which is essentially about learning facts, then memory processes are critical and instructional supports that encourage memory (e.g. optimal scheduling – see bottom left corner of table in Figure 13.2) would be best. But to the extent that the goals involve inducing some general rule or skill then optimal scheduling is unlikely to be a good principle to apply, instead a learning process that does some kind of induction and perhaps refinement would be more appropriate (e.g. worked examples). Whereas if the knowledge goal involves a deeper understanding and rationales, then supporting students in collaborative dialogue can be beneficial. Misapplying instructional principles will most likely be unproductive (as seen by the zeroes in Figure 13.2).

For example, the testing effect has been well studied by cognitive psychologists and postulates that testing enhances later retention more than additional study of the material (Roediger and Karpicke, 2006[18]). In contrast, educational psychology research originating in Australia (Sweller and Cooper, 1985[19]) and especially pursued in Europe (Paas and Van Merriënboer, 1994[20]; Renkl and Atkinson, 2010[21]) suggests students do too much practice and not enough study of worked examples. Theoretically, both have plausibility. The testing effect reflects a more general phenomenon and is more of a challenge for students, thus, produces “desirable difficulties”. Conversely, the worked example effect offers more guidance to reduce “cognitive load” and that premature practice encourages floundering and misconceptions.

Are these two positions really contradictory? First, both literatures show that an intermediate value (some combination of example study and problem-based test) is better than an extreme (i.e. all worked examples or all practice problems). Second, is the worked example effect even found in an online tutoring system where step-by-step support is available (as opposed to whole solution feedback), thus reducing cognitive load to the point that worked examples might be irrelevant.

In lab studies using a geometry tutor, students in the practice or testing condition generated a solution and explained their result with help from a glossary. They received feedback on both. In contrast, the worked example condition had half of the steps given as examples and they had to explain the worked-out steps with help from a glossary.

Lab results showed that worked examples improve both efficiency of learning (20% less instruction time to study worked examples then to do problems) and conceptual transfer (in one of the two lab studies) (Schwonke et al., 2009[22]).

Figure 13.2. Positive (+), neutral (0) and negative (-) outcomes of difference instructional principles employed to achieve the learning of different kinds of knowledge.

In classroom studies, adaptively fading examples to problems yielded better long-term retention and transfer (Salden et al., 2009[23]). Similar results were found with in vivo studies with chemistry tutors (McLaren et al., 2006[24]; McLaren et al., 2016[25]) and algebra tutors (Anthony, Yang and Koedinger, 2008[26]), always a reduction in time and sometimes improvement on a long-term retention test. Thus, the worked example effect generalises across domains and populations. Understanding the different goals will help with understanding the differences in learning processes. KLI does not simply identify content treatment interactions but provides theoretical guidance for what instructional treatments are most likely to work given a particular knowledge acquisition goal.

Scaling practical learning research

In the last 10-15 years, the US Department of Education has spent millions of dollars on big randomised field trials with about 10% having positive results. One reason for the dismal outcomes is a disregard for external validity issues of transfer. Moreover, and as illustrated in the testing vs. worked example effects, learning scientists, especially ones from different disciplines, do not always agree on what is best. Consequently, scaling science to practice is not simply taking learning theories and applying learning science to instructional design. The answer is not to apply learning science but to do data-driven iterative engineering. As depicted in the graphic in Figure 13.3, the iterative cycle involves: Start with existing theories, design explanatory models of learners and models of the desired expertise, use the models to design instruction, then collect data, interpret the data to gain insights, and redesign your models and your instruction. Repeat these loops of design, deploy, collect data, discover, (re)design, deploy and so forth.

Figure 13.3. Data-driven iterative engineering

A better social cyberinfrastructure is consistent with the idea of doing science in practice. This data-driven iterative process is needed in all institutions such that every school and university becomes a LearnLab (learnlab.org) where a culture of iterative improvement is fostered and assessments, data and analytics are shared. But it is not just about doing the loop of continuous improvement rather we need university administrators to foster a culture and to change incentive structures (e.g. credit for making improvements in courses not just for research done).

Scaling deep content analytics

Course data and learning theory are the forces behind making improvements to instruction and instructional design. A proven method for improving course design is doing a Cognitive Task Analysis (CTA) whose goal is to identify the underlying cognitive processes students need to learn a given task and to provide data for creating an accurate cognitive model. Research shows that courses modified by CTA produce better learning. For example, in a qualitative CTA, Clark et al. (2007[1]) found a 1.5 SD effect size when comparing a CTA modified course on catheter insertion for medical students to the traditional course (Velmahos et al., 2004[27]). One explanation for such results came after Clark ran a series of CTA studies. He observed and made the claim that 70% of what experts know is outside conscious awareness, that is to say, that most learning is implicit and garnered through imitation and practice (Clark et al., 2007[1]).

A more quantitative approach to CTA can be applied by using visual representations of student data (e.g. learning curves). When data is organised such that a good characterisation of the unobservable skills and concepts or a good cognitive model of the domain is available, then a smooth learning curve is produced. Bumpy curves suggest an opportunity for improvement as do flat curves. An upward blip in error rate in a curve (Figure 13.4A) often indicates that the current cognitive model is wrong – it is not accounting for critical elements of learning difficulty that students experience. A course analyst can thus identify and articulate a new critical component of knowledge that students need to acquire. Scientifically, such knowledge component (KC) discovery improves the fit of the model to the data, better accounting for error rates and producing smoother learning curves. Practically, such discovery leads to better learning support, including new instruction and new ways to practice the discovered KC.

LearnLab’s DataShop (Koedinger et al., 2010[28]) provides tools to help technology developers and learning engineers doing this kind of quantitative CTA. For example, the Performance Profiler (Figure 13.4) is a visualisation tool that can highlight discrepancies in error rates that may signal the need for new KC discovery. In Figure 13.4 we see a wide range of error rates (shown in dark grey) on tasks hypothesised to demand the same geometry planning skill – clearly some of these tasks (at the bottom) have greater knowledge demands than others (at the top).

Figure 13.4. Student performance data helps discover hidden skills and improve their learning

In this example, we found students struggled with finding the area of complex figures not because finding the area of individual shapes was difficult but because they were lacking the critical knowledge for planning solutions via selecting multiple relevant formula (Koedinger, Booth and Klahr, 2013[2]). New tasks were designed for the online tutoring that support students in learning this critical planning skill. These tasks isolated practice on such planning without wasting students’ time performing the execution steps they have already mastered. A classroom-based in vivo experiment comparing the adapted tutor to the original showed both much greater efficiency to mastery (25% less time) and greater effectiveness on a post assessment.

Scaling iterative course improvement

In summary, learning is invisible and both students and instructors need to be aware of illusions of learning. Data can break those illusions. Students need feedback on their progress, need formative assessment, and need long-term assessments and instructors need assessment data. We need learning engineers who 1) can use CTA techniques and data to deeply understand learning goals and how the human mind achieves them; and 2) can routinely employ learning science theories and methods to design and test new teaching techniques, in practice, through experiments that compare outcomes of these new techniques against outcomes of existing teaching. Once such experiments become part of standard practice in schools and universities, we will begin on a rapid path towards understanding which of the 200 trillion instructional options work best for which particular learning problem.

Policy implications

Learning science and technology are revolutionising education. Technology is already widening access to educational resources and making those resources increasingly more adaptive to student needs through advanced AI-fuelled algorithms. More importantly, practical learning science research is going to continue to unlock the mystery and power of human learning in ways that will have dramatic impact on education and, consequently, on the state of our world.

What do we need to do to make this learning revolution happen? We need to build social and technical infrastructure that better connects universities, educational technology companies, and especially schools such that learning science and practice is not a one-way technology transfer but a high-speed, internet-enabled many-way communication. We need to make schools and colleges, our institutions of learning, into learning institutions. Rather than being consumers of generic learning science, our schools must become producers of contextually specific and practical learning science. These institutions need government direction and financial support to transform themselves so as to regularly engage in continuous data-driven improvement. With the help of learning scientists, these institutions, not the learning scientists, will be the ones who discover what teaching techniques and technologies work best for the vastly different learning goals and student populations they serve. We need policies that foster adoption of continuous improvement processes that make it much easier for all educational stakeholders, from students and parents through teachers and administrators to educators and learning scientists, to collect and make use of high-quality data to inform which human and technology-based learning supports work best.

This institutional transformation will need to be fuelled by better higher education programmes that can produce the research-oriented teachers and learning engineers of the future. Collectively these new “learning workers” must have interdisciplinary expertise and collaboration skills to bring together scientific understanding of human psychology, technical skills of AI and machine learning, deep understanding of subject-matter domain content and how human brains acquire it, and methodological skills for designing experiments and using data towards continuous improvement. Just as science and technology have helped us to travel many times further and faster, from the early carriage to today’s jets, science and technology will also help us to learn many times better and faster.

References

[26] Anthony, L., J. Yang and K. Koedinger (2008), “Toward next-generation, intelligent tutors: Adding natural handwriting input”, IEEE Multimedia, Vol. 15/3, pp. 64-68, https://doi.org/10.1109/MMUL.2008.73.

[8] Bjork, R. (1994), “Memory and metamemory considerations in the training of human beings”, in Metacognition: Knowing About Knowing, MIT Press, Cambridge, MA, https://bjorklab.psych.ucla.edu/wp-content/uploads/sites/13/2016/07/RBjork_1994a.pdf.

[1] Clark, R. et al. (2007), “Cognitive Task Analysis”, in M. Driscoll (ed.), Handbook of Research on Educational Communications and Technology, https://www.learnlab.org/research/wiki/images/c/c7/Clark_CTA_In_Healthcare_Chapter_2012.pdf.

[10] Clark, R. and R. Mayer (2012), E-learning and the Science of Instruction: Proven Guidelines for Consumers and Designers of Multimedia Learning, Pfeiffer, San Francisco, CA.

[5] Eva, K. et al. (2004), “How can I know what I don’t know? Poor self assessment in a well-defined domain”, Advances in Health Sciences Education, Vol. 9/3, pp. 211-224, https://doi.org/10.1023/B:AHSE.0000038209.65714.d4.

[9] Kapur, M. and N. Rummel (2012), “Productive failure in learning from generation and invention activities”, Instructional Science, Vol. 40/4, pp. 645-650, https://doi.org/10.1007/s11251-012-9235-4.

[13] Klahr, D. and M. Nigam (2004), “The equivalence of learning paths in early science instruction: Effects of direct instruction and discovery learning”, Psychological Science, Vol. 15/10, pp. 661-667, https://doi.org/10.1111/j.0956-7976.2004.00737.x.

[15] Koedinger, K. and V. Aleven (2007), “Exploring the assistance dilemma in experiments with cognitive tutors”, Educational Psychology Review, Vol. 19/3, pp. 239-264, https://doi.org/10.1007/s10648-007-9049-0.

[28] Koedinger, K. et al. (2010), “A data repository for the EDM community: The PSLC dataShop”, in C. Romero et al. (eds.), Handbook of Educational Data Mining, http://cmu.edu/oli.

[2] Koedinger, K., J. Booth and D. Klahr (2013), “Instructional complexity and the science to constrain it”, Science, Vol. 342, pp. 935-937.

[3] Koedinger, K., A. Corbett and C. Perfetti (2012), “The Knowledge-Learning-Instruction framework: Bridging the science-practice chasm to enhance robust student learning”, Cognitive Science, Vol. 36/5, pp. 757-798, https://doi.org/10.1111/j.1551-6709.2012.01245.x.

[17] Lovett, M., O. Meyer and C. Thille (2008), “The Open Learning Initiative: Measuring the effectiveness of the OLI statistics course in accelerating student learning”, Journal of Interactive Media in Education, http://jime.open.ac.uk/articles/10.5334/2008-.

[24] McLaren, B. et al. (2006), “Studying the effects of personalized language and worked examples in the context of a web-based intelligent tutor”, in M. Ikeda, K. D. Ashley and T. W. Chan (eds.), Proceedings of the 8th International Confernce on Intelligent Tutoring Systems, Springer-Verlag, Berlin, https://doi.org/10.1007/11774303_32.

[25] McLaren, B. et al. (2016), “The efficiency of worked examples compared to erroneous examples, tutored problem solving, and problem solving in computer-based learning environments”, Computers in Human Behavior, Vol. 55, pp. 87-99, https://doi.org/10.1016/J.CHB.2015.08.038.

[6] Moos, D. and R. Azevedo (2008), “Self-regulated learning with hypermedia: The role of prior domain knowledge”, Contemporary Educational Psychology, Vol. 33/2, pp. 270-298, https://doi.org/10.1016/J.CEDPSYCH.2007.03.001.

[20] Paas, F. and J. Van Merriënboer (1994), “Variability of worked examples and transfer of geometrical problem-solving skills: A cognitive-load approach”, Journal of Educational Psychology, Vol. 86/1, pp. 122-133, https://doi.org/10.1037/0022-0663.86.1.122.

[16] Pane, J. et al. (2014), “Effectiveness of Cognitive Tutor Algebra I at scale”, Educational Evaluation and Policy Analysis, Vol. 36/2, pp. 127-144, https://doi.org/10.3102/0162373713507480.

[11] Pashler, H. et al. (2007), Organizing Instruction and Study to Improve Student Learning IES Practice Guide, National Center for Education Research, Institute of Education Sciences, US Department of Education, http://ncer.ed.gov.

[12] Pavlik, P. and J. Anderson (2008), “Using a model to compute the optimal schedule of practice”, Journal of Experimental Psychology: Applied, Vol. 14/2, pp. 101-117, https://doi.org/10.1037/1076-898X.14.2.101.

[21] Renkl, A. and R. Atkinson (2010), “Learning from worked-out examples and problem solving”, in Plass, J., R. Moreno and R. Brunken (eds.), Cognitive Load Theory, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511844744.007.

[18] Roediger, H. and J. Karpicke (2006), “Test-enhanced learning”, Psychological Science, Vol. 17/3, pp. 249-255, https://doi.org/10.1111/j.1467-9280.2006.01693.x.

[23] Salden, R. et al. (2009), “Worked examples and tutored problem solving: Redundant or synergistic forms of support?”, Topics in Cognitive Science, Vol. 1/1, pp. 203-213, https://doi.org/10.1111/j.1756-8765.2008.01011.x.

[22] Schwonke, R. et al. (2009), “The worked-example effect: Not an artefact of lousy control conditions”, Computers in Human Behavior, Vol. 25/2, pp. 258-266, https://doi.org/10.1016/J.CHB.2008.12.011.

[4] Singer, S. and W. Bonvillian (2013), “Two revolutions in learning”, Science, Vol. 339/6126, p. 1359, https://doi.org/10.1126/science.1237223.

[7] Sitzmann, T. et al. (2008), “A review and meta-analysis of the nomological network of trainee reactions”, Journal of Applied Psychology, Vol. 93/2, pp. 280-295, https://doi.org/10.1037/0021-9010.93.2.280.

[19] Sweller, J. and G. Cooper (1985), “The use of worked examples as a substitute for problem solving in learning algebra”, Cognition and Instruction,, Vol. 2/1, pp. 59-89, https://doi.org/10.2307/3233555.

[27] Velmahos, G. et al. (2004), “Cognitive task analysis for teaching technical skills in an inanimate surgical skills laboratory”, American Journal of Surgery, Vol. 187/1, pp. 114-119, http://www.ncbi.nlm.nih.gov/pubmed/14706600.

[14] Wieman, C. (2014), “Large-scale comparison of science teaching methods sends clear message”, Proceedings of the National Academy of Sciences, Vol. 111/23, pp. 8319-8320, https://doi.org/10.1073/pnas.1407304111.

End of the section – Back to iLibrary publication page