4. Global approaches to developing standard mortality tables for the provision of retirement income
This chapter reviews the mortality tables developed and used in 40 jurisdictions in the context of retirement income provision. It looks at how the tables are used in practice, and the methodologies used to develop the tables. It also compares the life expectancies calculated from the tables that are available compared to those of the population.
This chapter reviews the standard mortality tables developed and used in 40 jurisdictions, that is in all 38 OECD jurisdictions as well as Brazil and Peru. It first looks at whether standard mortality tables exist across jurisdictions and how they are used in practice. It then considers the methodology used to establish the base mortality assumptions, that is the level of mortality observed today. It subsequently discusses the different ways that the tables account for mortality improvements and the difference in modelling techniques employed. Finally, it compares the life expectancies calculated from the tables that are available compared to the general populations. Annex 4.A summarises the features of the standard mortality tables reviewed, and Annex 4.B provides additional details by jurisdiction.
The institutions most often responsible for the development of the standard mortality tables are regulatory/supervisory bodies, actuarial associations, or industry associations. Providers are often required to use these tables for particular valuations, at least as a minimum benchmark. Statistical associations and academics may also produce mortality tables used by providers, particularly where markets are less developed. However, these tables are normally only used as a reference for providers to benchmark any mortality assumptions they may develop themselves.1 Table 4.1 summarises the jurisdictions in which each type of institution is responsible for the development of (or takes the initiative to develop) a standard mortality table. It also indicates whether providers are required to use the tables developed as a reference, even if they may be allowed to use their own assumptions if deemed to be more appropriate.
For jurisdictions where separate tables exist for pension and annuity providers, different institutions may develop the standard mortality tables. This is the case in 6 of the 11 jurisdictions having distinct standard mortality tables for pensions and annuities.2
In jurisdictions where the regulatory or supervisory body is responsible for the development of mortality tables, providers are always required to use them in some manner. This is the case in 12 jurisdictions, though while the Finnish Government defines the mortality assumptions used to calculate pension income, these assumptions are not a fully-fledged mortality table, but rather a longevity coefficient that is calculated to adjust the retirement income of each subsequent cohort of pensioners to reflect recent improvements in life expectancy. In some jurisdictions, the regulator or supervisor only develops assumptions for either insurance or pensions, even where standard tables exist for both. For example, the Japanese regulator determines the tables to be used by pension providers.
Actuarial associations are the most common body taking responsibility for developing standard mortality tables. These tables are required to be used by providers in the majority of the 14 jurisdictions where this is the case. Here again, the associations may only develop mortality assumptions for either insurance or pensions. The actuarial associations of Germany and Japan develop assumptions used by annuity providers, whereas those in Italy develop the assumptions used by occupational pension providers. The table commonly used by annuity providers in Portugal was developed by the actuarial association in Switzerland.3 Where the tables are not required, they often serve as a benchmark or reference for providers to set their own assumptions, as in Australia and Ireland. While the New Zealand Society of Actuaries performs benchmark mortality studies that annuity providers can use to develop their own assumptions, they do not produce themselves complete mortality tables.
Industry associations are also commonly involved in the development of standard mortality tables. They are not required to be used by providers in half of the eight jurisdictions where this is the case.
It is less common for statistical institutes to be the main body producing a standard mortality table used by pension and/or insurance providers. The population life tables serve as a reference for providers in Estonia, Poland, and the Slovak Republic, but the annuity markets in these jurisdictions are not developed. In Portugal minimum funding requirements are based on tables for the French population, though in practice providers tend to use more recent tables than those required. In Switzerland, the mortality improvements commonly used by pension providers are developed in co-operation with the Federal Office of Statistics, although the base assumptions are developed by industry associations.
In a small number of jurisdictions (Czech Republic, Hungary, and Türkiye) academics have taken the initiative to develop studies or standard tables for the pensioner or annuitant population that providers can use as a benchmark. This has mainly been in response to the lack of existing mortality studies for these populations, and providers are not required to use these tables.
The majority of jurisdictions (23) have a standard mortality table that either pension or annuity providers are required to use. However, five of these jurisdictions do not require that those tables account for future mortality improvements (Colombia, Finland, Japan (pensions), Luxembourg, Portugal).
Usually, where providers are required to use standard mortality tables, they serve as a minimum basis for the calculation of reserves or technical provisions and funding requirements, though providers can adapt these assumptions if they are inadequate. However, the standard tables can also serve as a minimum requirement for establishing the retirement income that providers can pay. This is the case in Belgium, Finland, France, and Norway. The standard mortality tables also serve as the basis for calculating the allowed programmed withdrawals from pension funds in Chile, Colombia, and Peru. In the United States, the standard mortality tables are used for the calculation of the premium that pension providers must pay to be covered by the pension protection fund in addition to funding calculations.
The mortality assumptions for annuitants and pensioners are usually developed in two parts. The first step is to develop the base mortality rates that reflect the level of mortality at the time of the observed mortality experience. The second step is to develop assumptions around how mortality rates will decline over time, and thereby how life expectancy will improve going forward.
Ideally, there will be sufficient pensioner or annuitant data on which to calculate the current base mortality assumptions so that the estimated rates will accurately reflect the mortality of the population to which the assumptions will apply. The majority of jurisdictions (23) are able to develop mortality assumptions based directly on the pensioner and/or annuitant populations.4 However, this tends to be more common for pensioner populations, as annuitant populations tend to be much smaller.
4.2.1. Mortality at central ages
There is usually only sufficient mortality experience for pensioners or annuitants to calculate mortality rates for a central range of ages, typically within the rage of ages 50-95. For ages younger than this, mortality rates tend to be too low to observe a sufficient number of deaths, and older than this the number of observations tends to be too low for estimates to be reliable.
The raw mortality rates calculated from the experience of these populations for the central age range typically demonstrate significant volatility across ages due to their smaller size, and therefore need to be smoothed to ensure that mortality rates increase monotonically with age, in line with biological expectations. This is done using a smoothing function that allows for an exponentially increasing curve. The most common functions used are Gompertz and Whittaker-Henderson functions and their variations.
4.2.2. Extrapolation of mortality to younger and older ages
Mortality rates at younger ages are not always needed in the context of pensions and annuities, however many tables do include mortality assumptions for younger ages. The most common way is to apply an adjustment factor to the population mortality at younger ages to reflect the difference in mortality between the general population and the pensioner/annuitant population (e.g. German annuitants). Factors can also be applied to other mortality tables that reflect the expected shape of mortality at younger ages. The pensioner table in Canada, for example, applies a factor to an older mortality table to determine the mortality rates for younger ages. These factors would be based on the ratio of the pensioner/annuitant mortality to the mortality being referenced at other age(s). Alternatively, the mortality at younger ages can be extrapolated directly from the central age range (e.g. Brazil). In contrast, tables in the United Kingdom assume that the mortality at younger ages is the same as that observed in the population, under the assumption that the selection effect at younger ages is not material.
Mortality assumptions at the oldest ages are more relevant and important to adequately estimate in the context of retirement income. They are usually set using some sort of extrapolation technique. Many tables use models that are calibrated on the smoothed mortality rates of the last 10-15 ages in the central age range, and therefore result in a shape of mortality at the oldest ages that is cohesive with that for the central ages (e.g. Brazil, Chile, Costa Rica, France, Japan, Peru, and the United States). However, these types of models result a wide range of possible outcomes. As such, constraints are often imposed, such as a maximum age (e.g. France) or a maximum mortality rate (e.g. United States). Alternatively, mortality can be interpolated from the last ages in the central age range directly to a desired level of mortality (e.g. Colombia). A final approach is to graduate mortality rates from the central age range to an alternative set of mortality rates, such as the general population (e.g. United Kingdom) or an alternative mortality table (e.g. Canada pensioners). This latter approach is consistent with the assumption that mortality rates of different populations tend to converge with age, as the selection effect wears off and only the least frail of every population have survived.
Normally tables assume an ultimate age beyond which there will be no survivors. The most prevalent ultimate age assumed is 120 (Austria, Germany (insurance), Italy, the Netherlands, Slovenia, United Kingdom, and the United States), although a few jurisdictions assume 115 (e.g. Canada, Costa Rica, and Spain) and others assume an even older age (e.g. Belgium, France, and Japan). The minimum age assumed is generally 110 (e.g. Australia, Chile, Colombia, Mexico, and Peru), although the ultimate age for the table in the Czech Republic is lower at 103.
4.2.3. Accounting for selection effects
Where annuitant or pensioner mortality data is not sufficient to derive mortality assumptions directly from these populations, mortality rates for an alternative population may be used, which is typically the general population of the jurisdiction. In this case, a selection factor is normally applied to account for the lower pensioner/annuitant mortality compared to that of the general population. The selection factor is typically based on the experience in other jurisdictions, in particular the experience in Germany, Switzerland and the United Kingdom.
However, the reference population for which a selection factor is needed is not always the general population of the jurisdiction in which the tables apply. For example, Türkiye makes an adjustment to the mortality rates of all insured people to account for the difference between annuitants (who live longer) and those with life insurance (who die earlier) based on experience in the United States.5 A few jurisdictions tend to reference the population outside of their own jurisdiction, for example tables in Luxembourg refer to the European population, and tables used in Ireland tend to benchmark tables developed in the United Kingdom. Portuguese pension providers tend to rely on the tables for the French population, and their annuity providers on tables developed for Swiss group annuitants.
Some jurisdictions use alternative approaches to account for the selection effect. Rather than relying on experience in other jurisdictions to account for selection, the table for the centralised annuity provider in Lithuania approximates the selection effect by calibrating the mortality assumptions to the pensioners in the public system falling within the top two quintiles of pension income. Belgium takes an approximate approach by specifying an age correction, which assumes that an annuitant aged 65 will have the mortality of a younger Belgian.
Where selection is accounted for with a factor applied to the reference population mortality, the factors applied can vary by age and gender. Selection factors for the annuitant tables in Austria and Slovenia are gender distinct and decrease from around age 60, that is the annuitant mortality approaches that of the reference population after age 60. In contrast, the selection effect for Tax Qualified Pension Plan pensioners in Japan is a flat 15% for all.
Some jurisdictions do not apply selection factors despite the reference population being the general population. This is usually based on the justification that there is very high coverage of the system and the pensioner/annuitant population mortality should be very close to that of the whole population (e.g. Costa Rica, Finland, Iceland, the Netherlands).
4.2.4. Granularity of assumptions
At a minimum, all standard mortality tables have distinct assumptions for males and females.
Tables for the insurance sector more broadly usually distinguish assumptions by type of insurance, namely death and survivor (i.e. annuity) insurance (e.g. Brazil, Japan, the Slovak Republic) or group and individual (e.g. Austria, Sweden).
Different assumptions can also apply depending on the type of beneficiary. Some tables distinguish between active or deferred members and pensioners (e.g. Israel and Korea) or pensioners and their spouses/beneficiaries (e.g. Chile and Peru). Others allow for adjustments based on proxies for socio-economic status like annuity amounts, income, or sector of employment (e.g. Canada, the United Kingdom, and the United States).
4.2.5. Risk margins
Some standard mortality tables may also include risk margins on top of the best estimate mortality assumptions to ensure prudence in valuations and reserving. This can depend on the purpose of the calculation using the tables, as in Japan where additional reductions must be applied to the EPI table for wind-up valuations. While it is more common to apply a margin directly to the base mortality rates, some jurisdictions also apply margins to the improvement rates (e.g. Austria, Germany, and Norway).
Most standard mortality tables include not only base assumptions but also assumptions regarding expected future mortality improvements to account for future increases in life expectancy.6 However, 12 jurisdictions have not produced standard mortality improvement assumptions for either pensioners or annuitants (Brazil, Colombia, Estonia, Finland, Greece, Hungary, Luxembourg, New Zealand, Poland, Portugal, the Slovak Republic, and Türkiye). In addition, while improvement assumptions in Japan are developed for annuitants, pensioner tables do not account for them. Improvement assumptions are usually developed as part of the standard base table, but are occasionally developed separately and applied to a base table (Australia, Canada, Israel, Mexico, Switzerland, the United Kingdom, and the United States).
4.3.1. Data used
No standard mortality table calibrates the improvement assumptions solely on the pensioner or annuitant population directly.7 The majority base the mortality improvements on the historical mortality experience of the general population of the jurisdiction. However, England and Wales use improvements calibrated specifically to this population rather than the entire UK population. Occasionally, larger populations are considered, as is the case for the ATP in Denmark as well as in the Netherlands, who both use Western European experience to calibrate their improvement assumptions. France is one jurisdiction that uses the mortality experience of the annuitant population, where they apply a relational model that considers how the mortality of the annuitant population has evolved relative to the general population to project expected trends.
4.3.2. Projection model
As mortality improvements involve future predictions of how mortality will evolve, they must be estimated from a model that projects future mortality based on past experience. The approaches taken vary in their complexity, the underlying data used, and the extent to which user inputs shape the projections. Table 4.2 summarises the approaches taken by different jurisdictions to account for mortality improvements.
One of the most common, and simplest, approaches is to extrapolate future mortality rates based on a linear regression of historical log mortality rates. This type of regression is normally done by age or age group, and effectively assumes that the historical trend observed over the regression period will continue in the future. Eight jurisdictions adopt this approach to establish mortality improvement assumptions.
Alternative extrapolative models, such as Age Period Cohort (APC) models, which explicitly take into account the age-structure of mortality improvements, are also quite common and are implemented in eight jurisdictions. The most common of these models is the Lee-Carter model and its extensions, implemented in six jurisdictions (Chile, Costa Rica, Italy, Peru, Slovenia, and Sweden). The Lee-Carter model is a simple model, which can also be used for stochastic simulations, and incorporates age-dependent parameters as well as a parameter driving the overall mortality trend for all ages. While the table used by pension providers in Austria relies on an alternative methodology – a Markov Chain Monte Carlo method – the results are very close to those using the Lee-Carter model. Iceland uses the Cairns-Blake-Dowd (CBD) model, which is adapted primarily for older ages and has an overall trend parameter as well as a parameter that determines the slope of the mortality across ages in any given year.
One approach that has more recently been gaining popularity is the interpolation of improvement rates between recent improvements – derived from a graduation of historical mortality experience – and some assumption regarding a lower long-term rate to which improvements should converge. This approach was initially advanced by the model developed by the Continuous Mortality Investigation (CMI) of the Institute and Faculty of Actuaries (IFoA) in the United Kingdom. Variations on this approach have been adopted in seven jurisdictions (Austria (insurance), Canada, Chile, Ireland (CMI), Israel (CMI), United Kingdom (CMI), United States (pensions). The Menthonnex model is an alternative graduation approach and is used by pension providers in Switzerland. It relies on time-dependent variables to model the age structure of mortality over time, and implicitly assumes the ‘rectangularisation’ of survival over time, that is a higher concentration of deaths around the modal age of death. As such, the model results in slowing mortality improvements over time.
Some jurisdictions implement multi-population models to be able to calibrate expected trends that account for the relationship between the evolution of multiple sets of mortality rates. Multi-population models are used in three jurisdictions. The ATP in Denmark and the Royal Dutch Actuarial Association use stochastic models that model short-term deviations between the mortality experience of their respective general populations and the larger Western European population, with the assumption that the difference in the trend of these two populations will eventually stabilise. The Dutch model also ensures coherence between the projections of the male and female populations. While the French tables also rely on a multi-population model, they take a different approach with the objective to account for any differences in the evolution of mortality between the general French population and that of the annuitants.
Other jurisdictions rely on the mortality projections of the statistical institutions which generally account for other demographic factors, namely fertility and migration, though these projections may be somewhat adapted. The latest tables developed by the Institute of Actuaries in France use a relational model referencing the mortality projections of Institut National de la Statistique et des 󠆰Études Économiques (INSEE). The tables developed for insurers in Italy rely on ISTAT projections along with a Lee-Carter model. In Mexico, the tables use mortality improvement assumptions based on the projections of CONAPO.
Less common are simplified and approximate approaches to indirectly account for mortality improvements. Annuity providers in Japan and Korea use tables that apply a static factor to reduce the base mortality rates estimate in the level of life expectancy that historical trends in mortality improvements would imply for the future. Belgium takes an alternative approach for the MR-FR table by specifying an age reduction of five years that intends to account for both selection and future mortality improvement.
Occasionally, additional improvements are added to those implied by the model to account for potential selection effects and the expectation that pensioners or annuitants may experience higher mortality improvements than the population on average. The table used by annuity providers in Germany includes an additional 0.2% annual improvement, and the one used by annuity providers in the United States includes an additional 0.4% annual improvement for ages 65-82, grading to an additional 0.2% for ages 87 and over.
4.3.3. Convergence to a long-term improvement rate
Mortality improvements developed for standard mortality tables are moving more and more towards an approach that assumes that the recently observed mortality improvements will eventually converge to a lower long-term rate. This reflects the expectation that the relatively high improvements observed particularly over recent decades are not sustainable in the longer term. Table 4.3 summarises assumptions used by different tables regarding the long-term rate of improvement.
In in their basic form, extrapolative models rely on the assumption that mortality improvements observed in the past will continue indefinitely into the future. However, some jurisdictions adapt these models to rely on the model outputs for the short term only, and interpolate the mortality between these assumptions and an assumed long-term rate. For Germany and Lithuania, who both rely on linear extrapolative models, long-term improvement assumptions are based on longer-term historical trends in the respective jurisdictions. In Germany, this is calculated as 75% of the historical trend over the period 1972-99, subject to minimum and maximum boundaries of 1% and 3%. In Lithuania, the long-term rate is calculated as the historical experience over 1995-2017. The long-term improvement assumption in Iceland is defined as 1%. In Switzerland a long-term rate is not explicitly set, rather the interaction of the model parameters results in a gradual slowdown of mortality improvements. The model used by annuity providers in Austria does not set an explicit long-term rate either, rather the model assumes that the initial mortality improvements will be halved over the next 100 years to avoid unreasonably low mortality rates in the long term.
Jurisdictions using an interpolative approach to project graduated historical experience to a long-term improvement rate explicitly set that rate by definition. In Canada and Chile, the rate is set to 1%, and to 1.35% for the United States. In Ireland and the United Kingdom – who rely on models developed by the CMI – the long-term improvement assumption is input by the user, though for the latest CMI model the default assumption is 1.5%. Israel also relies on the CMI model, but sets long-term improvement assumptions at 1.25% for males and 1.5% for females.
Multi-population models can incorporate a long-term assumption regarding the relationship of mortality improvements between populations. The models used in Denmark and the Netherlands reference Western European experience as a basis for their long-term improvement assumptions, and assume that the local mortality improvements will mirror those of larger and similarly developed countries in the long term.
The period of convergence is a key assumption for models explicitly assuming a long-term improvement rate. This is set at 20 years in Canada and Chile. In Iceland, convergence is delayed for 20 years, at which point improvements are assumed to converge to the long-term rate over a period of 25 years. For improvement assumptions used by pension providers in the United States, the convergence period is 20 years across cohorts but only 10 years across periods. The period/cohort convergence periods also vary for the CMI model used in the United Kingdom, though the period length and shape can be adjusted by the user and younger cohorts are subject to shorter convergence periods.
4.3.4. Mortality improvements at older ages
As with setting the base mortality assumptions, mortality improvement assumptions are often only directly calibrated for a range of central ages due to the lack of sufficient data at older ages on which to establish a robust trend. In general, mortality improvements at older ages are assumed to be lower than those for central ages.
A common approach is to assume a linear decline in mortality improvements to 0% at a certain age. This is done in Canada, Chile, Iceland, Peru, the United Kingdom and the United States. The tables used by annuity providers in Austria assume rather an exponential decline. In contrast, the tables used by annuity providers in Germany maintain positive improvements at older ages, specifying a minimum initial mortality improvement of 1% and a long-term improvement of 0.76%.
4.3.5. Dimension of the mortality table
The dimension of the mortality table is a consideration with respect to the complexity of using the table to model and value liabilities. While models now can typically incorporate two-dimensional mortality assumptions, some jurisdictions continue to reduce tables to a single dimension. Table 4.4 summarises the different types of approaches and provides examples of the tables taking each approach.
The most common approach is to have a single dimensional base mortality table (rates by age for a given year) coupled with a two-dimensional mortality improvement scale (annual improvements by age and year). This allows improvement rates to change over time, in particular where lower long-term rates are assumed. Where the population used to calibrate the base mortality and mortality improvements are the same, the model can be fully integrated and produce both current and future mortality rates directly (e.g. in the Netherlands). Having a single-dimensional improvement scale, where improvements by age remain constant in the future, is also common.
A few jurisdictions, however, still reduce the mortality table to a single dimensional base table even when they intend to account for future mortality improvements. These are sometimes provided only as alternative assumptions where it is not possible to use a two-dimensional table, as in the Czech Republic, Italy and Slovenia. The reduction of the tables to a single dimension is typically done using the age-shift method, where the mortality rates for a specific cohort are specified, and an age adjustment is applied to other cohorts. For example, the mortality of a 65-year-old from the 1960 cohort could be equivalent to the mortality of someone two years younger from the 1955 cohort to account for the higher life expectancy of the younger cohort. In contrast, the Belgium MR-FR table is a periodic table, where an age shift of five years is applied to account for both the selection factor and future mortality improvements, i.e., a 65-year-old is assumed to have the same cohort life expectancy as the period life expectancy of a 60-year-old today.
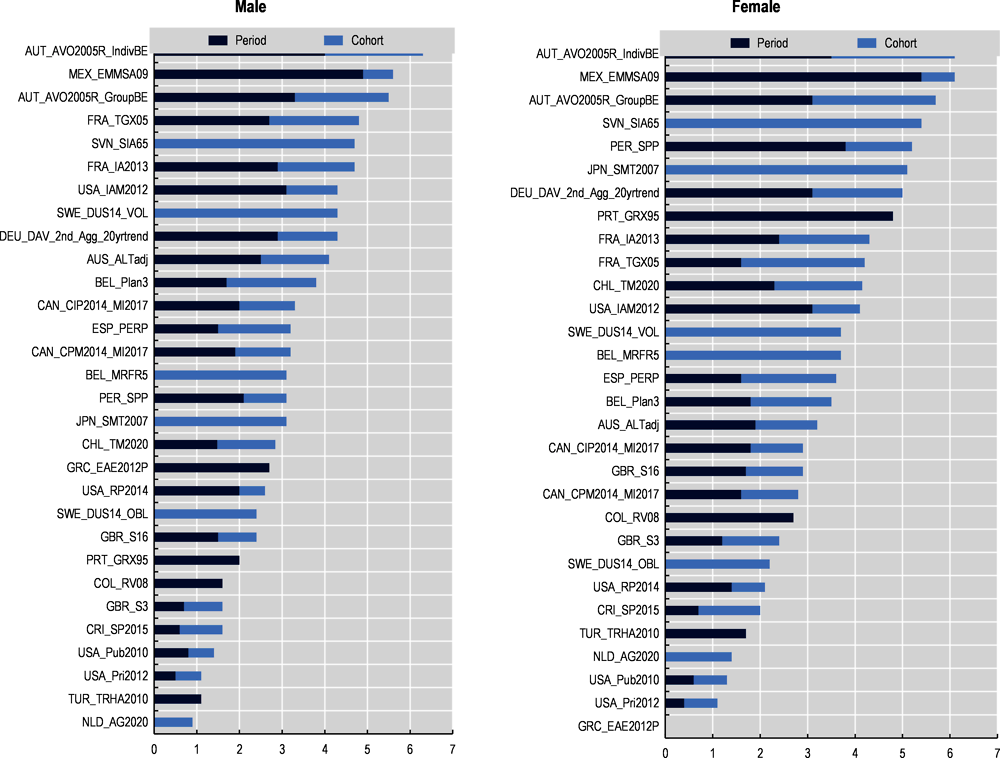
Comparing the life expectancies given by the standard mortality tables for pensioners and annuitants with the life expectancy of the general population shows the large impact that selection and mortality improvements can have.8 Selection refers to the tendency for the pensioner or annuitant population to have a higher life expectancy than the general population, and mortality improvements refer to the expected future gains in life expectancy for each cohort. Table 4.5 shows the life expectancies at age 65 for the general population and standard mortality tables in each jurisdiction. The life expectancy for the standard tables is provided both accounting for future improvements (cohort) and without them (period). The difference between the period life expectancy of the standard table and the population life expectancy is the impact of selection.
Figure 4.1 shows more clearly the additional years of life expectancy at age 65, relative to the general population, that result from accounting for selection and mortality improvements. Selection adds on average around 2 to 2.5 additional years of life expectancy at age 65, while mortality improvements add around an additional 1.5 to 2 years. The average of both components combined is around 3 to 3.5 years.
The impact of selection is related to the proportion of the population that is covered by the arrangement. The larger the proportion of the population that pensioners or annuitants represent, the closer the mortality of the pensioner or annuity population will be to that of the general population, and thereby the smaller the selection effect will be. Figure 4.2 demonstrates this tendency for a select sample of countries. Indeed, the higher the coverage, the lower the impact that selection has on life expectancy.
For the jurisdictions included in this report, standard mortality tables are developed by regulators/supervisors, actuarial associations, industry bodies, statistical institutions and/or academics. Where providers are required to use these mortality tables, they are most often developed by the regulator/supervisor.
There are two components to mortality tables. The first is the level of mortality observed today, or the base mortality assumptions, and the second is the projection of future mortality improvements to account for expected increases in life expectancy.
The base mortality assumptions are either based directly on the level of mortality observed for the pensioner or annuitant population or on the experience of the general population. In the latter case, an adjustment factor is usually needed to account for selection effects and the fact that the mortality of the pensioner or annuitant population tends to be higher than the general population. Due to the lack of mortality experience at higher ages, mortality rates are normally extrapolated to some ultimate age beyond which no survivors are expected, commonly around age 120. Tables typically distinguish mortality rates at least by gender, but can also specify them by product or plan type, type of beneficiary, or by socio-economic indicator.
Mortality improvement assumptions require a model to project future mortality rates from past observed experience to determine the expected future increases in life expectancy. Most often these models are extrapolative, either linearly extrapolating historical trends in the log mortality rates or using another extrapolative model such as Lee-Carter that takes into account an age structure for the improvement rates. Another common approach is to interpolate mortality improvements from smoothed historical experience to some long-term rate of mortality improvement in the future. Occasionally projections rely on demographic projections of statistical institutes or use an approximate approach such as a simple reduction factor. The most accurate approach with respect to the dimension of the mortality table is to allow mortality improvements to vary by age and year, but some jurisdictions take a simplified approach, adjusting a single vector of mortality rates to account for the different mortality across cohorts.
The life expectancies given by standard mortality tables are typically significantly higher than the life expectancy for the general population due to the selection effects and future expected mortality improvements. On average, these increase life expectancy at age 65 by around 2.5 years and 1.5 years, respectively, resulting in a life expectancy at age 65 around 3.5 years higher for pensioners/annuitants relative to the period life expectancy of the general population.
References
[48] AG Projections Life Tables Working Group (2020), Projection Table AG2020, https://www.ag-ai.nl/view/39421-Projection.
[57] Ahčan, A. et al. (2012), Slovenian Annuity Tables.
[71] American Academy of Actuaries (2011), 2012 Individual Annuity Reserving Table.
[38] ANIA (2014), Le basi demografiche per rendite vitalizie A1900-2020 e A62.
[5] Australian Government Actuary (2018), Australian Life Tables 2010-12, https://www.aga.gov.au/publications/life_table_2010-12/ (accessed on February 2021).
[13] Canadian Institue of Actuaries (2015), Canadian Insured Payout Mortality Table 2014 (CIP2014).
[14] Canadian Institute of Actuaries (2017), Task Force Report on Mortality Improvement.
[15] Canadian Institute of Actuaries (2014), Final Report: Canadian Pensioners’ Mortality.
[20] Centro Centroamericano de Poblacion (2018), Proyección de la mortalidad de Costa Rica 2015-2150.
[18] Centro Centroamericano de Población (2018), Tablas de mortalidad de Costa Rica 2010-2015.
[21] Cipra, T. (n.d.), Generation Life Tables for Czech Pension Funds.
[67] CMI (2021), CMI Mortality Projections Model: CMI_2020.
[65] CMI (2018), Proposed S3 Series Mortality Tables.
[66] CMI (2017), CMI Mortality Projections Model: CMI_2016.
[64] CMI Annuities Committee (2020), Final “16” Series pension annuity in payment mortality tables.
[45] Commissariat aux Assurances (2012), Lettre circulaire 03/5 du Commissariat aux assurances relative aux bases techniques en assurance-vie, https://www.caa.lu/uploads/documents/files/Circ03_5_coord_2012.pdf.
[9] Commission des Pensions Complementaires (2011), Règlement fixant les tables e mortalité pour la conversion e capital en rente, https://www.fsma.be/sites/default/files/legacy/sitecore/media%20library/Files/fsmafiles/advorg/advorgcapwn/fr/advice34.pdf.
[46] CONSAR (2019), Estadísticas del Registro Electrónico de Planes de Pensiones 2019, https://www.consar.gob.mx/gobmx/aplicativo/sirepp/(S(vpnj1u5tif1srhtv4qmib5ix))/Docs/Estadisticas_Registro_2019.pdf.
[56] Correia, T. (2018), A Mortality & Longevity Study: The Portuguese Case.
[12] De Oliveira, M. et al. (2016), “Mortality tables for the Brazilian insured population”, Revista Brasileira de Estudos de População, Vol. 33/3, pp. 653-677, https://doi.org/10.20947/s0102-30982016c0010.
[58] de Vicente Merino, A. et al. (2000), Proyeccion y estudio e una poblacion. El papel de mortalidad.
[27] Deutschen Aktuarvereinigung (2018), Herleitung der DAV-Sterbetafel 2004 R für Rentenversicherungen, https://aktuar.de/unsere-themen/lebensversicherung/sterbetafeln/2018-01-24_DAV-Richtlinie_Herleitung_DAV2004R.pdf.
[31] Félag íslenskra tryggingastærðfræðinga (2020), CBD líkan fyrir breytingar á lífslíkum, https://actuaries.is/utgefid-efni/danar-og-eftirlifendatoflur/.
[51] Finans Norge (2013), Nytt beregningsgrunnlag for kollektiv pensjonsforsikring.
[24] Finnish Centre for Pensions (2019), The life expectancy coefficient for 2020 according to the Employees Pension Act, https://www.etk.fi/wp-content/uploads/2020/05/The-life-expectancy-coefficient-for-2020.pdf.
[29] Hablicsekné, M. (2011), A nyugdíjban, nyugdíjszerű ellátásban részesülők halandósága (2006), https://nyugdijbiztositas.tcs.allamkincstar.gov.hu/m/pdf/nyugdjasok_halandsga_2006_hnrm.pdf.
[30] Hollósné Marosi, J. and L. Molnár D. (2015), “Az öregségi nyugdíjasok halandósága. A nyugellátási összeg, a nyugdíjazási életkor és a halandóság összefüggései Magyarországon, 2004-2012”, Közgazdasági Szemle, Vol. 62/12, pp. 1258-1290, https://doi.org/10.18414/ksz.2015.12.1258.
[16] Howard, B. (2014), CPM 2014 Mortality Tables.
[10] IAA Mortality Working Group (2013), Country Report Belgium, https://www.actuaries.org/CTTEES_TFM/Documents/MWG_Singapore_Item3_Country_Report_Belgium.pdf.
[50] International Actuarial Association (2018), Country Report - Norway, https://www.actuaries.org/IAA/Documents/WG_MWG/Meetings/Berlin_2018/Minutes/Additional_docs/10d_Country_Report_May2018.pdf.
[34] International Actuarial Association (2017), Country Report - Israel, https://www.actuaries.org/CTTEES_TFM/Documents/Budapest_April2017/15_Country_Report_Israel_April2017.pdf.
[41] International Association of Actuaries (2017), Country Report - Japan, https://www.actuaries.org/CTTEES_TFM/Documents/Chicago_2017/Country_Report_JAPAN.pdf.
[54] International Association of Actuaries (2016), Poland Mortality Report 1/2016, https://www.actuaries.org/CTTEES_TFM/Documents/StPetersburg-May2016/Documents_appended_to_Minutes/25.3_Country_Report_Poland_2016-05-23.pdf.
[63] International Association of Actuaries (2016), Turkey Mortality Report, https://www.actuaries.org/CTTEES_TFM/Documents/Cape_Town_Nov2016/8_MortalityReport_Turkey.pdf.
[36] Israeli Association of Actuaries (2018), Report of the Mortality Research Committee of the Israel Association of Actuaries on Mortality Improvements in Israel.
[22] Jarner, S. and E. Kryger (2013), “Modelling Adult Mortality in Small Populations: The Saint Model”, ASTIN Bulletin, Vol. 41/2, pp. 377-418, https://doi.org/10.2143/AST.41.2.2136982.
[7] Kainhofer, R. (2019), Zur Angemessenheit der Rententafel AVÖ 2005-R, https://avoe.at/wp-content/uploads/2019/10/Rententafel_AVOe2005R_Ueberpruefung2019.pdf.
[6] Kainhofer, R., J. Hirz and A. Schubert (2018), AVÖ 2018-P: Rechnungsgrundlagen für die Pensionsversicherung, http://avoe.at/wp-content/uploads/2018/08/AVOe2018P_Dokumentation.pdf.
[8] Kainhofer, R., M. Predota and U. Schmock (2005), The New Austrian Annuity Valuation Table AVO 2005R, http://avoe.at/pdf/mitteilungen/H13_w3.pdf.
[43] Korea Institute of Finance (2013), The Growth and Development of the Korea Insurance Development Institute (KIDI).
[62] Menthonnex, J. (2015), Estimation des durées de vie par génération: Evolution 1900-2150 et tables de mortalité par génération 1900-2030 pour la Suisse.
[39] Mitchell, O. and D. McCarthy (2001), Estimating International Adverse Selection in Annuities.
[49] New Zealand Society of Actuaries (2019), Longevity in New Zealand: Implications for Retirement Income Policy.
[1] OECD (2022), Life expectancy at 65 (indicator), https://doi.org/10.1787/0e9a3f00-en (accessed on 22 December 2022).
[3] OECD (2019), “Coverage of funded and private pension plans”, in Pensions at a Glance 2019: OECD and G20 Indicators, OECD Publishing, Paris, https://doi.org/10.1787/983bdeef-en.
[55] OECD (2019), OECD Reviews of Pension Systems: Portugal, OECD Reviews of Pension Systems, OECD Publishing, Paris, https://doi.org/10.1787/9789264313736-en.
[44] OECD (2018), OECD Reviews of Pension Systems: Latvia, OECD Reviews of Pension Systems, OECD Publishing, Paris, https://doi.org/10.1787/9789264289390-en.
[47] OECD (2016), OECD Reviews of Pension Systems: Mexico, OECD Reviews of Pension Systems, OECD Publishing, Paris, https://doi.org/10.1787/9789264245938-en.
[35] OECD (2014), Mortality Assumptions and Longevity Risk: Implications for pension funds and annuity providers, OECD Publishing, Paris, https://doi.org/10.1787/9789264222748-en.
[37] Ordine Nazionale degli Attuari (2012), I percettori di rendite in Italia: analisi della mortalitá dal 1980 al 2009 e previsioni al 2040.
[17] Ortiz, F., M. Villegas and A. Zarruk (2013), “Tablas De Mortalidad (Mortality Tables)”, SSRN Electronic Journal, https://doi.org/10.2139/ssrn.2351968.
[28] Pasdika, U. and J. Wolff (2005), Coping with Longevity: The New German Annuity Valuation Table DAV 2004 R.
[11] Paul, J. (2009), Quotients de mortalité prospectifs par sexe et unisexes, https://www.plan.be/uploaded/documents/201002040818570.wp200918.pdf.
[25] Planchet, F. (2007), Tables TGH / TGF 05: Construction.
[23] Rahandusministeerium (2015), Kohustusliku kogumispensioni väljamaksete analüüs, https://www.rahandusministeerium.ee/sites/default/files/document_files/finants/ii_samba_valjamaksete_analuus.pdf.
[4] Rice Warner (2018), Exploring Retiree Mortality, Institute of Actuaries Australia, https://actuaries.asn.au/Library/Opinion/2018/AIExploringRetireeMortalityFINAL.pdf.
[19] Rosero Bixby, L. and A. Collado Chaves (2008), “Tablas de mortalidad, jubilación e invalidez, Costa Rica 2000-2005”, Población y Salud en Mesoamérica, Vol. 6/1, https://doi.org/10.15517/psm.v6i1.4537.
[53] SBS (2018), Desarrollo de tablas de mortalidad applicables al sistema privado de pensiones de Peru.
[74] Society of Actuaries (2021), Mortality Improvement Scale MP-2021, https://www.soa.org/globalassets/assets/files/resources/experience-studies/2021/2021-mp-scale-report.pdf.
[69] Society of Actuaries (2020), Mortality Improvement Scale MP-2020.
[72] Society of Actuaries (2019), Pri-2012 Private Retirement Plans Mortality Tables Report.
[73] Society of Actuaries (2019), Pub-2010 Public Retirement Plans Mortality Tables Report.
[68] Society of Actuaries (2014), RP-2014 Mortality Tables Report.
[33] Society of Actuaries in Ireland (2020), Calibration of the CMI model for Ireland.
[32] Society of Actuaries in Ireland (2019), Irish Insured Lives Mortality Investigation (IILMI), https://web.actuaries.ie/sites/default/files/2019-03/190306%20-%20Irish%20Insured%20Lives%20Mortality%20Investigation%20Report%20Final.pdf.
[70] Society of Actuaries RPEC (2022), RPEC 2022 Mortality Improvement Update, https://www.soa.org/4a9cd8/globalassets/assets/files/resources/research-report/2022/rpec-mortality-improvement.pdf.
[59] Svensk Försäkring (2014), Försäkrade i Sverige: livslängder och dödlighet, prognoser 2014-2070.
[52] The Financial Supervisory Authority of Norway (2013), Nytt dødelighetsgrunnlag i kollektiv pensjonsforsikring (K2013), https://www.finanstilsynet.no/contentassets/fdcb5b465a1a434e9eb9579d33ef03ce/nytt-doedelighetsgrunnlag-i-kollektiv-pensjonsforsikring-k-2013.pdf.
[26] Tomas, J. and F. Planchet (2016), Construction et Validation des Références de Mortalité de Place.
[60] Wan, C. and L. Bertschi (2015), “Swiss coherent mortality model as a basis for developing longevity de-risking solutions for Swiss pension funds: A practical approach”, Insurance: Mathematics and Economics, Vol. 63, pp. 66-75, https://doi.org/10.1016/j.insmatheco.2015.03.025.
[2] WHO (2019), Life tables: Life tables by country Peru, https://apps.who.int/gho/data/view.searo.61280?lang=en.
[61] Willis Towers Watson (2019), SLI® Swiss pension plan. Benchmarking study 2019.
[40] Yamazaki, H. (2017), SMT 2018 (Standard Mortality Table 2018).
[42] Yamazaki, H. (2015), 2007 SMT (2007 Standard Mortality Tables).
Annex Table 4.A.1 summarises the main features of the standard mortality tables reviewed in this chapter.
Country context for standard mortality tables
Although life annuities are available as an option at retirement in the context of the Australian superannuation defined contribution system, the annuity market in Australia remains very small.
The Actuaries Institute of Australia has published an indicative reference mortality table for each gender that can be used as a benchmark for the level of mortality for pricing and reserving. However, it is based on data from a limited number of providers and therefore cannot be relied upon by itself.
The Australian Government actuary publishes mortality improvements based on the experience of the Australian population.
Technical details
The Actuaries Institute of Australia engaged the consulting firm Rice Warner to develop mortality tables that could be used as a reference for the development of retirement income products in 2018. Unfortunately, they found that there were not sufficient data on annuities in Australia to develop tables directly from this population. They therefore derived a selection factor to apply to the Australian general population data from the annuitant mortality experience in the United Kingdom. Their proposal also involved a second adjustment to the Australian Life Table (ALT) 2010-12 that intends to account for the lower mortality in Australia by increasing the ratio of annuitant to population mortality applied to the life table. The selection factor is calculated arbitrarily by taking half of the observed mortality difference between the Australian and UK populations, and applying this to the observed mortality difference between the UK annuitant and general population. The tables intend to provide a reasonable range for annuitant mortality in Australia (Rice Warner, 2018[4]).
The mortality improvement assumptions published by the Australian Government actuary are based on observed population trends over the last 25 and 125 years, up to 2010-12 (Australian Government Actuary, 2018[5]).
Country context for standard mortality tables
The Austrian Association of Actuaries (AVÖ) publishes mortality tables for the calculation of technical provisions for both pension funds and pension annuity insurance.9
The AVÖ 2018-P, published in 2018, provides the calculation basis to assess the obligations of pension funds. The ÖFdV GmBH, a subsidiary of AVÖ, sells and licenses the calculation bases. The tables account for retired, disabled, and survivor benefits (Kainhofer, Hirz and Schubert, 2018[6]).
The AVÖ 2005-R, published in 2005, provide the calculation basis for pension annuity insurance. The tables are intended for use by insurance companies with guaranteed products. There are tables for group and individual annuitants for both genders. The Calculation Basis Working Group of the AVÖ regularly assesses these tables for adequacy. The last assessment in 2019 concluded that the table continues to be adequate and should still be used for the calculation of private pension insurance in Austria (Kainhofer, 2019[7]).
Technical details
The AVÖ 2018-P is based on data from Pension Insurance Institutions (PVA), the Farmers Social Insurance Institution (SVB), the Social Insurance Institution for the Commercial Economy (SVA), and the Insurance company for railway and mining (VAEB). It allows for a full stochastic valuation of obligations by using a Markov model with transition probabilities among the states of retired, disabled, and survivor. The base table refers to the year 2008, and is smoothed using a Whittaker Henderson formula. The Heligman Pollard formula is used to extrapolate mortality to the oldest ages. Mortality improvements are based on the Austrian population from 1980-2017, and is projected forward using a Markov Chain Monte Carlo method that assumes no reversion of the trend to a long-term rate. The results of this model are very close to the results using the Lee-Carter model to project future mortality improvements (Kainhofer, Hirz and Schubert, 2018[6]).
The annuity valuation table AVÖ 2005-R is based on Austrian population data, with a central year of 2001, as there is not sufficient mortality experience for Austrian annuitants on which to base the tables. Two tables are developed: a 2nd order best estimate table, and a 1st order table that includes substantial safety margins for model and parameter risk. The 1st order table includes an additive addition to the base mortality of 0.003 and a multiplicative factor of approximately 1.1 to the trend assumptions.
The selection factors used to adjust the Austrian life tables were developed in reference to the Swiss ERM/F 1999 tables for annuitants, the German DAV 2004-R tables for annuitants, and the old AVÖ 1996 tables. The selection factors follow a function that is constant at 0.8 until age 40, declining linear to age 60 before converging with a quadratic function to 1 at age 100. There are different selection factors by gender for individual and group annuitants, the latter group’s mortality being closer to that of the general population. The selection effect does not account for selection in terms of the amount of the annuity, only in terms of individuals. The table provides rates to age 120.
The mortality improvement assumptions are based on 30 years of Austrian population data, from 1972. The initial trend is derived from the Lee-Carter model. The trend slows over time in a non-linear fashion, halving its initial value over 100 years, in order to limit the table and avoid death probabilities near zero in the far future. Improvements for old ages assume a slow exponential decline to zero, with an upper limit at younger ages of 5%. Additional adjustments ensure monotonicity (Kainhofer, Predota and Schmock, 2005[8]).
A one-dimensional table has also been developed using the age-shift method, but it is not recommended for use over the two-dimensional generational table.
Country context for standard mortality tables
Since 2003, the Financial Services and Markets Authority (FSMA) requires insurers to use a minimum mortality table based on the Belgian population, the MR-FR, to calculate annuity income and technical provisions. Since 2011, an age correction of five years is required to account for the selection factor and future mortality improvements. These tables do not explicitly take future mortality improvements into account (Commission des Pensions Complementaires, 2011[9]).
The Federal Planning Bureau has since developed generational tables that explicitly account for mortality improvements of the Belgian population.10 The FSMA suggests insurance companies to use this for annuities by applying an age correction of three years to account for the selection factor (Commission des Pensions Complementaires, 2011[9]).
The Institute of Actuaries in Belgium set up a mortality working group, with one subgroup investigating mortality in the second pillar of the pension system, including annuities.11 Notwithstanding, the annuity market remains extremely small.
Technical details
The MR-FR tables are defined through input parameters to the Makeham formula specified in the law (IAA Mortality Working Group, 2013[10]).
The mortality projections of the Federal Planning Bureau project Mortality improvements forward with an exponential formula based on smoothed trends derived from a linear regression of the logarithm of the historical rates since 1970. The method is modified for older ages to provide more stability at these ages (Paul, 2009[11]).
Country context for standard mortality tables
The mortality tables for the Brazilian insurance market are the result of a joint initiative between the government, the insurance companies, the Brazilian Association of Insurance and Pension Companies (FenaPrevi). The first table, the BR-EMS-2010 was based on insured experience from 2004-06. These tables were updated in 2015 to incorporate experience from 2007-12. Tables are constructed by gender and type of insurance (death/survivor). The Brazilian regulator SUSEP considers these tables to be the standard reference for mortality tables for insurance providers (De Oliveira et al., 2016[12]).
Technical details
The mortality experience used to develop the BR-EMS-2010 tables represents approximately 80% of the insured population, which in turn represents around 22% of the Brazilian population. The calculation of the mortality rates are weighted towards the most recent observations, and rates at the middle ages are smoothed with moving averages. Mortality at the youngest and oldest ages are extrapolated using the Heligman Pollard model.
Country context for standard mortality tables
The Canadian Institute of Actuaries (CIA) develops and publishes mortality tables that serve as an expected reference for the mortality assumptions used for pensions and insurance in Canada. The Actuarial Standards Board (ASB) generally promulgates the tables for the purposes of calculating termination values and solvency funding.
In 2014, the CIA published the first mortality tables based on Canadian pensioner data, the CPM2014. Tables are gender distinct, and also include separate tables for public and private sector experience. The ASB has promulgated the use of these tables to calculate the commuted values for the termination of benefit entitlements within defined benefit plans.
In 2015, the CIA published the first mortality table based on Canadian experience for payout annuities, the CIP2014.
The base tables are used in conjunction with mortality improvement scales that the CIA develops separately. The first improvement scale based on Canadian data was the CPM-B mortality improvement scale developed in 2014 alongside the CPM2014 table (Canadian Institue of Actuaries, 2015[13]). The improvement scale is two-dimensional, although a one-dimensional approximation was also published. Then in 2017 the CIA published the MI-2017 improvement scale, which updated the CPM-B improvement scale published in 2014. While the former scale was based on Canadian pensioner data from the CPP and the QPP, the new scale reflects the mortality improvements of the whole Canadian population (Canadian Institute of Actuaries, 2017[14]). The ASB now promulgates this latter scale for use along with the base CPM2014 table.
Technical details
The CPM2014 mortality tables are based on the mortality data of individuals having registered pension plans (RPP) over 1999-2008. Rates are calculated on an amount basis rather than individual exposures, and size adjustment factors are provided to adjust the mortality expectations for different pension levels. Deaths are adjusted to account for mortality improvements to 2014 rather than using the central year of observation as the base year. Exposures and deaths are also weighted by industry to reflect the distribution across industries for all Canadian DB plans so as to be more representative of the Canadian experience on average. Raw mortality rates for central ages are graduated using the Lawrie variation of the Whittaker Henderson model. Mortality rates for younger ages are derived by applying a factor to the insurance table CIA9704 and interpolating the two curves with a 5th order polynomial. Rates for the oldest ages use those obtained directly from the Human Mortality Database (HMD), up to a maximum age of 115. Tables are split between public and private sector (Canadian Institute of Actuaries, 2014[15]; Howard, 2014[16]).
The CIP2014 is constructed using both individual and joint annuitant mortality experience having policies with an annualised income less than CAD 72 000. The experience used ranges from age 70 to 100 and covers the years 2000-11. The central mortality rates are smoothed using the Whittaker Henderson model. Ages over 106 are those developed for the CPM2014 table, and interpolated with a 4th degree polynomial. (Canadian Institue of Actuaries, 2015[13]).
The CPM-B mortality improvement scale was developed alongside the CPM2014 table, and is based on Canadian pensioner data from the C/QPP. Short-term rates are based on ten years of mortality experience. The short-term rates are linearly interpolated from 2012 to a long-term rate in 2030 of 0.8% up to age 82, decreasing gradually to 0% at age 115 (Canadian Institute of Actuaries, 2014[15]).
The MI-2017 improvement scale uses the Whittaker Henderson model to smooth historical rates. The initial improvement rate is the smoothed rate two years before the final observed year. It uses cubic interpolation to project to a long-term improvement rate of 1% to age 90, which grades down linearly to 0.2% to age 100 and 0% at age 105. The convergence period is 20 years for ages 60-80, grading linearly down to 10 years for ages below 40 (Canadian Institute of Actuaries, 2017[14]).
Country context for standard mortality tables
The pension and insurance regulatory bodies in Chile, the Superintendence of Pensions (SP) and the Financial Market Commission (CMF), are jointly responsible for developing the mortality tables used in the context of the Chilean pension system. The tables for pensioners are used to calculate the allowed levels of programmed withdrawals and to determine the required reserves that insurers must hold to back their annuity business. The tables must be reviewed and updated on a regular basis.
The TM-2014 was developed in 2014. They are gender distinct, with separate tables for beneficiaries and the disabled. These tables were updated in 2020, and the new TM-2020 table will be required from July 2023.12
Technical details
The TM-2014 tables were based on non-disabled annuitant, pensioner and beneficiary data from 2008-13. Those having a pension below the basic solidarity pension were excluded. A separate table was produced for female pensioners and survivors, while a single table was produced for male pensioners and survivors. Central ages were smoothed using the Whittaker-Henderson model. Younger ages were based on the Chilean population mortality, and older ages were extrapolated using the model that demonstrated the best fit for each table.
Mortality improvements were based on the Lee-Carter model calibrated with 30 years of Chilean population data. To facilitate the implementation of applying the improvement scale, it was reduced to a one-dimensional table for each gender by age. Improvements over 80 were linearly graduated down to 0% at age 100.
The [draft] TM-2020 tables use broadly the same methodology for the base rates as the TM-2014 tables for data covering 2014-19. However, the new tables change the way in which they account for future mortality improvements. Rather than a one-dimensional improvement scale, a two-dimensional scale is developed based on Chilean population data from 1992-2016. Initial improvement rates are determined by the 2016 improvements after smoothing the historical data with a two-dimensional Whittaker Henderson model to age 90. Initial improvement rates are assumed to decline linearly to 0% at age 105. The initial rates are extrapolated to a long-term rate over 20 years using a cubic polynomial. The long-term improvement rate is set at 1% for ages up to 90, and then declines linearly to 0% at age 105.
Country context for standard mortality tables
Resolution 1 555 of July 2010 imposes a legal requirement for the standard mortality table RV08 to be used for the calculation of programmed withdrawals and annuity reserves within the Colombian pension system. This table is based on annuitant mortality experience in Colombia.
Technical details
The RV08 mortality tables is based on Colombian annuitant and pensioner experience over the period 2005-08. Central ages are smoothed according to Makeham’s law. Mortality at the oldest ages are determined using a second order polynomial setting the mortality rate to 0.6 at age 106 and 1 at age 110. Morality for younger males is determined using the female table as a reference. No safety margins are included (Ortiz, Villegas and Zarruk, 2013[17]).
Country context for standard mortality tables
The National Council for the Supervision of the Financial System approves the mortality tables that must be used for the calculation of technical provisions for annuities. Since 2014 these tables have accounted for mortality improvements. The most recent tables, the SP-2015, were updated in 2019. Superintendence of Pensions (SUPEN) calculates the mortality improvements to be used with the tables.
Technical details
The SP-2015 tables are based on the mortality experience of the Costa Rican population data over the period 2010-15 (Centro Centroamericano de Población, 2018[18]). An earlier study concluded that the mortality of the pensioner population did not differ substantially from that of the general population, and the use of census data for the construction of mortality tables for pensioners was appropriate (Rosero Bixby and Collado Chaves, 2008[19]). To construct the SP-2015 tables, mortality rates based on census data are smoothed and extrapolated to a maximum age of 115 using the Gompartz model (Centro Centroamericano de Población, 2018[18]). The mortality improvements are based on the Lee-Carter model calibrated to Costa Rican population data over the period 1950-2015 (Centro Centroamericano de Poblacion, 2018[20]).
Country context for standard mortality tables
There is no legal requirement for the mortality table that pension funds or insurance companies use for the calculation of the technical provisions for annuity products. Typical practice has been to base the mortality tables on the life tables developed for the Czech population. Nevertheless, the Charles University of Prague has developed a generational life table for the Czech pensioner population as a reference.
Technical details
The Czech Generational pensioner mortality table is based on the Czech life tables over the period 1900-96 and ages through 103. The trend is based on a linear regression of the log mortality rates, with some adjustments to ensure monotonicity and reasonableness of results. Selection factors are based on data from Munich Re, and the same factors are used for both genders. They decrease to age 60, and increase again to 0.75 from age 75. The tables include a safety margin at a 99% confidence level. A one-dimensional table is also provided based on the age-shift method from the base cohort born in 1955 (Cipra, n.d.[21])
Country context for standard mortality tables
The Danish Financial Supervisory Authority (FSA) develops a benchmark mortality table every year for pension funds and insurance companies based on data provided by the Danish Centre of Health and Insurance. While providers are allowed to use their own mortality assumptions, they must justify any deviation from the benchmark table.
While the ATP is also subject to the requirement to use the FSA tables, they justify developing their own tables by showing that the mortality experience of ATP members differs significantly from the FSA tables. The ATP uses the Saint model to model the mortality used for pricing and valuation exercises. They update their assumptions every year with the latest data available.
Technical details
The FSA’s benchmark tables are based on pensioner and insured data supplied on a voluntary basis, covering around 50-60% of the Danish population. Mortality improvements are based on 20 years of experience of the general Danish population, extrapolated linearly for each cohort.
The Saint model used by the ATP is a multi-population stochastic model that projects the mortality of a sub-population with reference to a larger population. The reference population is made up of the pooled experience of a group of Western European countries. The Saint model aims to overcome the challenge of modelling mortality for small populations and to also allow for improvements for different ages to move in different directions. The long-term trend is based on a reference population, while the short-term trend is based on a stationary time series model fitted to the deviations in mortality experience between the sub-population and the reference population. Variability in projected mortality comes from both variability of the trend and variability in the difference in mortality from the reference population, the latter which is subject to boundaries so that the deviations do not become too large (Jarner and Kryger, 2013[22]).
Country context for standard mortality tables
The only standard tables that exist in Estonia are the life tables published by Statistics Estonia for the general population. Insurers are allowed to determine their own assumptions for the valuation of pension contracts. The mortality assumptions used tend to be somewhat more conservative than the population figures. While insurers are free to set assumptions, they are obliged by law to share 50% of the technical profits with their policyholders and beneficiaries (Rahandusministeerium, 2015[23]).
Country context for standard mortality tables
Mortality rates are used to calculate the life expectancy coefficient that determines the amount of retirement income that a retiree will receive from the partially funded TyEl pension scheme. The purpose of this coefficient is to adjust the amount of retirement income downwards to reflect longer life expectancies for each cohort.
Technical details
The life expectancy coefficient is calculated each year for the cohort aged 62 in reference to the average population mortality over the last fve years relative to the population mortality in 2009, up to a maximum age of 100. The coefficient for 2020 is based on unisex mortality rates over the period 2014-18. Expected mortality improvements are not accounted for. The coefficient assumes a discount rate of 2% (Finnish Centre for Pensions, 2019[24]).
Country context for standard mortality tables
French legislation requires that pension funds and annuity providers use the TGH/TGF 05 mortality tables as a minimum basis to value their liabilities and to price annuities.
The French Institute of Actuaries have more recently built a standard mortality table (IA2013) intended to be used by insurers as a reference to assess their best estimate mortality assumptions in the context of Solvency II.13
Technical details
The TGH 05 (males) and TGF 05 (females) are based on French annuitant mortality data over the period 1993-2005. The base table was smoothed with a Gompartz model. Ages beyond 95 were extrapolated using a variation on a quadratic extrapolation. Younger ages were based on population data. Future mortality rates were projected using a relational model referencing French population data from 1962 to 2000 smoothed and extrapolated with cubic splines. Projections were adjusted to maintain a coherent relationship between the annuitant and population mortality (Planchet, 2007[25]).
The base tables rely on insured data from 2007-11, smoothed with a generalised linear model adjusted for maximum likelihood. Rates for ages over 95 were extrapolated using a method proposed by Denuit and Goderniaux imposing a maximum age constraint of 130. The mortality trend is projected via a non-parametric model referencing the INSEE projections of French population data to 2060 (Tomas and Planchet, 2016[26]).
Country context for standard mortality tables
The German Institute of Actuaires (DAV) produced the DAV 2004 R standard table. The DAV reviewed the tables over 2016 and 2017, and determined that they are still appropriate for the valuation of new business (Deutschen Aktuarvereinigung, 2018[27]). The German supervisor prescribes these tables, with a margin for conservatism, as a minimum standard for the valuation of pension and annuity liabilities of life insurers, non-regulated Pensionskassen and insurance-type Pensionsfonds. However, these entities may use their own tables if justified as more appropriate.
The firm Heubeck-Richttafeln-GmbH periodically produces generational mortality tables based on the mortality experience of German employees. While not required, these tables are used by some institutions to assess obligations of occupational pension arrangements. The latest tables were released in 2018.14
Technical details
The DAV 2004 R table is based on insured experience over the period from 1995 to 2002. In addition to the base tables, select and ultimate tables for benefits in payment are also produced to reflect the higher selection effect in the five years following the commencement of annuity payments. Raw mortality rates are smoothed using for central ages using the Whittaker Henderson model. Selection factors are based on the ratio of the smoothed mortality rates during the selection period relative to the population mortality. Ultimate mortality rates are based on all available annuitant data. Mortality rates for younger ages derived from the population mortality based on the ratio of the ultimate rates to the general population. Mortality is extrapolated to age 120 using a logistic model.
Two tables are produced: a 2nd order table reflecting best estimate expectations, and a 1st order table containing safety margins. The 1st order table includes a margin for volatility risk of around 6-7%, and a 10% margin for parameter risk, resulting in a total margin of 15.6% for males and 16.5% for females.
Initial mortality improvements are based on Western German population experience from 1990 to 1999. For the 2nd order best estimate tables, the initial trend is extrapolated to a long-term trend based on 75% of the German population experience from 1972-99, within the boundaries of a maximum of 3% and a minimum of 1% at the oldest ages. The tables assume an additional 0.2% annual improvement to reflect expectations that the life expectancy of the insured population will improve at a faster rate. The period of convergence is left to the user. 1st order tables assume that the mortality improvement will continue at the initial rate, and also assume an additional 0.25% annual improvement as a safety margin for parameter risk (Pasdika and Wolff, 2005[28]).
Country context for standard mortality tables
The Bank of Greece previously published the mortality tables that life insurance companies were required to use to calculate their reserves. They produced tables for both survival and annuity products, but did not include mortality improvement assumptions. Annuity providers are now free to use any mortality table that represents their best estimate assumptions, so the Bank of Greece no longer develops mortality tables.
For pension providers, secondary legislation is planned to allow pension providers to use their own mortality tables.
Country context for standard mortality tables
No standardised mortality table exists in Hungary, though some academic studies have investigated in detail the mortality of pensioners in the country, including old-age pensioners in the public system. Hablicsekné (2011[29]) looks at the mortality and life expectancy of pensioners across different types of benefits (old-age, survivor, disability) and constructs abridged mortality tables to age 90 for each benefit type and gender. Hollósné and Molnár (2015[30]) investigate the socio-economic differences in pensioner mortality by assessing mortality by gender and size of pension.
Country context for standard mortality tables
In 2019, the Icelandic Actuarial Association updated the life tables for the Icelandic population. In 2020, they approved a new approach to forecasting future mortality improvements for pension fund members.
Technical details
The base mortality tables are based on life tables produced by the Icelandic Actuarial Association for data covering the period 2014-18. Projections of future mortality improvements are done with the Cairns-Blake-Dowd model calibrated to Icelandic population data over the period 1981-2018 for the age range 45-89 for males and 50-94 for females. Improvements at younger ages assume the improvement of a 45-year-old male, and older ages assume improvements decreasing to 0% at old ages. Improvements are assumed to begin declining after 20 years, and converge to 1% at age 85 over the following 25 years (Félag íslenskra tryggingastærðfræðinga, 2020[31]).
Country context for standard mortality tables
The Society of Actuaries of Ireland (SAI) produces mortality experience studies and projections to serve as a reference for actuaries, including for annuitants. However, they do not produce Irish-specific mortality tables. In practice, Irish experience is benchmarked to the mortality experience of the United Kingdom and the studies carried out by the Continuous Mortality Investigation of the UK Institute and Faculty of Actuaries. They most recently found that the Irish annuitant experience is most closely approximated by the PXL08 tables based on UK pensioner data in 2007-10 (Society of Actuaries in Ireland, 2019[32]). The SAI also recently published a report in which they calibrated the CMI model for Ireland (Society of Actuaries in Ireland, 2020[33]).
Technical details
The SAI took two approaches to calibrate the CMI model to Irish experience. The first calibrated the model directly to Irish population mortality experience for age 20 to 100 and years 1977-2017. They reduced the smoothing parameters, which determine how much weight the model gives to the most recent observations, by 1.22 for females and 1.28 for males from the default of 7. This decision was to reflect the smaller size of the Irish population and the higher volatility of historical experience. The second approach was a simplified approach that calibrated the CMI model with data from England and Wales, but adjusted the initial improvement to reflect the differences between the mortality improvements experienced in the two populations. The latter approach tended to underestimate the mortality improvements in Ireland (Society of Actuaries in Ireland, 2020[33]).15
Country context for standard mortality tables
The Commissioner of Capital Markets, Insurance and Savings produces the mortality tables that pension funds must use to value pension liabilities. Separate tables are produced for pensions in deferral and pay-out. However, pension funds are allowed to use their own assumptions so long as they can justify that their assumptions are more appropriate.
Since 2001, the Commissioner also mandates the table that must be used to calculate the reserves for insurance products having a Guaranteed Annuity Option (GAO), or a guaranteed annuity conversion rate. These tables were based on the mortality experience of pension funds with an additional selection factor to account for the expected lower mortality of annuitants of insurance companies. In 2016, the government Actuary performed the first experience analysis of Israeli annuitants to inform the construction of the mortality table (International Actuarial Association, 2017[34]).
Regulations require that both pension funds and insurance companies account for future mortality improvements. Assumptions are based on the Israeli population using the CMI model that assumes a convergence to a long-term improvement rate of 1.25% for males and 1.5% for females. The latest factors were revised in 2018. A separate table is developed for the male cohorts born between 1929 and 1945 who have historically experienced higher mortality improvements than other cohorts. Assumptions more conservative than the best estimate assumptions are required for reserving (OECD, 2014[35]).
The Central Bureau of Statistics (CBS) has also produced projections of mortality since 2012 for the Israeli population.
In 2018 The Israeli Association of Actuaries, at the request of the Commissioner, published a report to investigate the projection of mortality improvements in Israel. The investigation studied several different models, but did not recommend a single model and the development of a mortality tables for the pensioner and annuitant populations was outside of its remit (Israeli Association of Actuaries, 2018[36]).
A major challenge identified with respect to setting mortality assumptions in Israel is the large rates of immigration in the country, which reduces the stability of the demographic characteristics of the population.
Country context for standard mortality tables
Various institutions construct mortality tables that can be used as a reference for assumption setting for pensioners and annuitants in Italy.
The Italian National Order of Actuaries performed a study to develop mortality tables for Italian pensioners based on pensioner data over the period 1980-2009 and projected to the year 2040 using several different models (Ordine Nazionale degli Attuari, 2012[37]).
The Association of Italian Insurance Companies (ANIA) constructed mortality tables for life annuitants in 2014. These two-dimensional A1900-2020 tables are used to derive a one-dimensional table based on an age-shift method referencing the 1962 cohort. Separate tables have been constructed for immediate, deferred, and group life annuities by gender (ANIA, 2014[38]).
Technical details
The base tables reference Italian pensioner mortality experience in 2009 for pension plans managed by both public and private institutions. The working group implemented several projection models calibrated on Italian population data from 1980 to 2009. These models included the Lee-Carter model, the log-bilinear Poisson model, the Renshaw Haberman model with cohort effect, and the CMI model (pre-2018 version) implementing the Age-Period-Cohort model (Ordine Nazionale degli Attuari, 2012[37]).
The mortality tables are based on the ISTAT projections of population data, which use the Lee-Carter model and account for demographic factors such as fertility and immigration. The ISTAT projections were extended to age 120 for the 2020 cohort through a linear extrapolation of the log mortality rates. Selection factors are based on UK pensioner experience (the “life office pensioners”) (ANIA, 2014[38]).
Country context for standard mortality tables
Regulation requires that pension schemes use the EPI mortality tables for funding and valuation requirements. These tables are based on the experience of the public Employee’s Pension Insurance, and are updated every five years. They do not explicitly take mortality improvements into account. While the tables can be used as-is for going concern valuations, wind-up valuations require that the EPI mortality rates be reduced by 5% for males and 7.5% for females. Reductions in the mortality assumptions for going concern valuations are subject to a maximum of 10% for males and 15% for females (OECD, 2014[35]).
Tax Qualified Pension Plans (TQPP) are required to use a different mortality table to value their liabilities. It is specified as 85% of the mortality of the Japanese Life Table for the population, though it is not clear whether the most recent Life Table must be referenced (Mitchell and McCarthy, 2001[39]).
Insurance companies are required to use the Standard Mortality Table (SMT), developed by the Institute of Actuaries of Japan (IAJ) to calculate annuity reserves. The latest of these tables was the SMT 2007. The IAJ reviews the adequacy of this table in each year, and released an updated version of the table, the SMT 2018, however the updated tables only apply to life and medical insurance, and the valuation of annuity reserves must continue to use the SMT 2007 tables (Yamazaki, 2017[40]).
The Life Insurance Association of Japan (LIAJ) performs periodic studies on the mortality of insured lives, but does not disclose the results of these evaluations (International Association of Actuaries, 2017[41]).
Technical details
The mortality for the SMT 2007 based on the 19th Life Table for the Japanese population, representing the mortality in the year 2000. Mortality rates for ages over 94 are extrapolated with a cubic function to age 122 for males and 126 for females. Mortality improvement calculations are based on Japanese population data over the period 1980-2000 by gender, five-year age group and cause of death. The table provides the mortality for the 1960 cohort. Based on these improvements, a reduction factor is then applied of 85% for central ages and 60% for younger ages to account for the expected mortality improvements (Yamazaki, 2015[42]).
Country context for standard mortality tables
The Korean Insurance Development Institute (KIDI) is legally responsible for the construction of mortality tables for the life insurance sector since 1989. Insurers are required to use these tables for reserve calculations, though they can use their own experience for pricing. The KIDI updates the tables every three years. The rates are based on the mortality experience of the insurance sector (Korea Institute of Finance, 2013[43]). The tables used for annuitants implicitly account for expected future mortality improvements and include additional safety margins. Three separate tables are applicable to the pensioner and annuitant populations. The EMT table for pensioners applies to pensioners before retirement, and is only used to ensure that the employer has sufficient reserves to meet its liabilities. The EMT table for life insurance applies to annuitants before retirement. The EMT table for annuitants applies to both populations after retirement.
Country context for standard mortality tables
There are no standard mortality tables in Latvia, and annuity providers are free to set their own assumptions. In practice, the assumptions used account for future mortality improvement. However, the populations on which the tables are based are not necessarily the annuitants themselves nor the Latvian population. The tables used by annuity providers tend to result in a life expectancy around two years greater than the period life tables for the Latvian population (OECD, 2018[44]).
Country context for standard mortality tables
Individuals having accumulated at least EUR 10 000 in the retirement savings accounts for the second pillar pension in Lithuania are required to purchase an annuity. Since 2020, a centralised annuity provider managed within the State Social Insurance Fund Board (Sodra) issues these annuity contracts. To price and value the annuity liabilities, it uses a mortality table based on Lithuanian pensioner mortality and the mortality improvements of the Lithuanian population.
Prior to 2020, private insurers provided the annuity products for the second pillar system. They are still allowed to provide voluntary annuities. There is no standard mortality table for the private sector. Providers tend to calculate their mortality assumptions using a selection factor based on UK experience and mortality improvements of the Swedish population.
Technical details
The centralised annuity provider’s mortality table is based on the mortality experience of Lithuanian pensioners having a pension level within the top two income quintiles. Short-term improvements are based on the latest 10 years of mortality experience of the Lithuanian population, calculated with a linear regression of the log mortality rates. These rates converge linearly over 20 years to a long-term improvement assumption based on Lithuanian mortality experience over 1995-2017.
Country context for standard mortality tables
Insurers are required to use mortality tables that are based on recent European population mortality to calculate their technical provisions, adapted to the risk that the insurers face, that is longevity risk in the case of annuities. Insurers can adapt the mortality tables if they are able to justify the differences (Commissariat aux Assurances, 2012[45]).
Country context for standard mortality tables
There are no specific requirements regarding mortality assumptions for occupational pension plan sponsors. In practice, providers commonly used the EMSSA97 table that is based on population mortality experience and improved only to 2011 for males and 2013 for females based on projections by CONAPO (OECD, 2014[35]). However, since 2017 the EMSSA-09 table is more commonly used in more pension plans’ valuations (CONSAR, 2019[46]).
Annuity providers are required to use, as a minimum, the EMSSAH-CMG-09 to value their liabilities, the same table that they use for pricing. They are also required to take future mortality improvements into account. Reserve requirements stipulate that an additional 2% be set aside to cover technical provisions. The base mortality for the tables are based on data from IMSS and ISSSTE over the period 1998 to 2008. Mortality improvement assumptions are based on CONAPO’s projections for the Mexican population (OECD, 2016[47]).
Country context for standard mortality tables
The Royal Dutch Actuarial Association publishes a new mortality table every two years, with the latest table published in 2020. This table intends to serve as a reference for pension and insurance companies to develop their own mortality assumptions. Tables are based on the mortality of the Dutch population and include future expected mortality improvements.
Technical details
Since 2014, the Royal Dutch Actuarial Association uses the Li-Lee two-population stochastic model to forecast future mortality improvements. The model projects Dutch mortality in reference to a larger population of European countries having a similar prosperity level to the Netherlands, which makes the model less sensitive to annual volatility of Dutch mortality experience. The model projects and overall trend of the reference population following a random walk with a drift, and the deviation of the Dutch mortality from the reference population is explicitly modelled with a first order autoregressive process. Both genders are modelled simultaneously, and since 2016 the model also incorporates a correlation in experience between males and females. The European trend is based on data since 1970. The model assumes that the difference in mortality between the Dutch population and the reference population will converge to an absolute value that is based on mortality experience since 1983 (AG Projections Life Tables Working Group, 2020[48]).
Country context for standard mortality tables
The annuity market in New Zealand is very small, and insurers typically develop their own mortality assumptions. The New Zealand Society of Actuaries has published mortality investigations on insured lives, but does not itself produce graduated mortality tables (New Zealand Society of Actuaries, 2019[49]).
Country context for standard mortality tables
Finance Norway has developed the mortality table K2013. The Financial Supervisory Authority requires the use of this table as a minimum basis for the calculation of technical provisions for and pricing for collective pension insurance provided by life insurers and pension funds. Finance Norway monitors these tables against observed mortality experience (International Actuarial Association, 2018[50]). The table is available for purchase only.
Technical details
The K2013 table is based on mortality experience over the period 2005-09 of pension members in Finians Norge’s member companies. Rates are projected to 2013. Additional security margins of 12% of the base mortality and 10% of mortality improvements are included (Finans Norge, 2013[51]). The mortality rates incorporate mortality improvements by age and gender (The Financial Supervisory Authority of Norway, 2013[52]).
Country context for standard mortality tables
The Superintendence of Banking, Insurance and Private Pension Funds Administrators of Peru (SBS) is responsible for the development of the mortality table used in the context of the Peruvian Private Pension System (SPP). These tables are used for the calculation of annuity reserves and the level of programmed withdrawals that old-age pensioners can withdraw from their pension savings. The latest tables are the first to be based specifically on the Peruvian population and to incorporate future mortality improvements. Providers have been required to use them since 2019.
Technical details
The mortality tables for healthy lives are based on Peruvian old-age pensioner and annuitant data within the SPP over the period 2010-16. Central ages are smoothed using the Whittaker Henderson model. Extrapolation to older ages relies on the Makeham and Gompartz models for females and males, respectively. Younger ages are extrapolated as a function of the mortality rates for the general Peruvian population. Mortality improvements are modelled with the Lee-Carter model calibrated to Peruvian population data over the period 1991-2016 through age 80. Improvement rates decrease linearly to 0% between the ages of 80 and 100 (SBS, 2018[53]).
Country context for standard mortality tables
Official population mortality tables produced by the Central Statistical Office of Poland (GUS) are commonly used, though individual companies may apply adjustment factors to these tables to reflect their own experience. GUS does not produce projections of future mortality. Companies may develop their own improvement assumptions or rely on academic studies to develop them (International Association of Actuaries, 2016[54]).
Country context for standard mortality tables
Regulation issued by the Portuguese supervisor specifies a minimum funding scenario for pension funds, whose purpose is to establish a minimum ‘safety net’ funding rule, based on the mortality table TV 73/77. The TV 73/77 is an old mortality table for annuities based on the French population over 1973-77. The assumptions to be used in the minimum funding scenario, however, are currently under revision and a public consultation has been launched with a proposal to update the mortality table assumption to the TV 88/90. For funding purposes, providers already commonly use the more recent TV88/90 table. No mortality improvements are taken into account (OECD, 2019[55]).
Life insurers often use the GKX95 tables, though in practice they do tend to adjust the mortality assumptions used based on the mortality experience of their portfolios. The GKX95 tables are based on the experience of group annuitants of Swiss insurance companies over the period 1986-90 (Correia, 2018[56]).
Country context for standard mortality tables
The Statistical Office of the Slovak Republic has constructed a mortality table based on based on the Slovak population structured by age and gender. In practice, insurance companies often construct their own mortality tables. The annuity market is not yet developed in the Slovak Republic.
Pension fund providers are required for the purpose of pension benefit statements to use the projected mortality tables published on the website of the Statistical Office of the European Communities to calculate pension forecasts. However, for the actual calculation of annuity income and liabilities, providers use their own tables.
Country context for standard mortality tables
Regulation specifies the mortality tables the pension companies must use to calculate their reserves. For contracts issued before 1 October 2016, they must use the German table DAV 1994R. For contracts issued since then, new tables SIA65 based on Slovenian data must be used. These tables serve as a minimum basis for the reserves of insurance companies (Ahčan et al., 2012[57]).
Technical details
The base mortality rates for the SIA65 are based on the Slovenian population of 2010 adjusted with selection factors. Selection factors are derived from experience in the United Kingdom and Germany. Additional selection factors are applied for the immediate annuity table (SIA65), which is the same as the deferred annuity table (SDA65) from age 60 (Ahčan et al., 2012[57]).
Mortality improvements are based on Slovenian population data since 1945, projected forward using a Poisson log bilinear model similar to the Lee-Carter model. The projected improvements are reduced to a one-dimensional table using the age shift method. The maximum age for the table is 120 (Ahčan et al., 2012[57]).
Country context for standard mortality tables
The Insurance Supervisor in Spain recommends the use of the PERM/F 2000 tables for the valuation of annuity contracts. Separate tables are applicable for policies in force before and after 1 November 2000. The tables are based on the Spanish population mortality, adjusted by a selection factor based on the Swiss population and incorporating mortality improvements (OECD, 2014[35]).
Technical details
The base mortality for the PERM/F 2000 tables is derived from the Spanish population mortality in 1990 improved to the year 2000. Improvement factors are based on an analysis of Spanish mortality improvements from 1960 to 1990. Selection factors are derived based on the Swiss EVK90 tables for group insurance, with factors increasing over age 50 to 100 (de Vicente Merino et al., 2000[58]).
Country context for standard mortality tables
The Swedish Pensions Agency uses mortality tables based on Swedish population data to calculate technical provisions and annuity income for the Premium Pension. Technical provisions are based on best estimate mortality with a loading factor.
For private pension providers, the Swedish Insurance Companies Industry Organisation publishes mortality tables (DUS14) based on data from Swedish life insurance companies. Separate tables are produced for voluntary insured (life insurance) and compulsory insured (occupational pensions). These tables are used in practice to calculate technical provisions.
Technical details
Mortality assumptions are based on Swedish population data forecasted by Statistics Sweden, and use cohort mortality by decade rather than individual age. Forecasts are updated every three years. Mortality rates are smoothed with the Gompertz Makeham law, and extrapolated linearly from age 100.
The DUS14 tables are based on Swedish insured and pensioner data over the period 2001 to 2012. Mortality improvements are modelled with a Lee-Carter model calibrated to Swedish population data over the period 1968-2012 (Svensk Försäkring, 2014[59]).
Country context for standard mortality tables
Occupational pension funds, which are mandatory in Switzerland, tend to rely on either the Standard BVG/LPP tables (for private pension funds) or the VZ tables (for public pension funds), potentially adjusted to reflect the mortality experience of the specific plan (Wan and Bertschi, 2015[60]). The latest BVG/LPP tables (the LPP 2020) are based on pensioner mortality from 15 large pension funds over the period 2015-19. These tables are available for purchase only. Most pension funds rely on the BVG tables, however only around half of them account for future mortality improvements, though one study indicated that two-thirds of pension funds did so (Willis Towers Watson, 2019[61]).
Mortality improvement assumptions developed by Menthonnex, in collaboration with the Federal Office of Statistics (OFS), tend to be used when mortality improvements are assumed. The Menthonnex mortality improvements are based on Swiss population mortality experience from 1900-2013, projected to 2 150 (Menthonnex, 2015[62]).16
Life insurers tend to rely on the ERM/F 2013 tables to value annuity liabilities, which are based on Swiss life insurance experience between 1981 and 2011.
Technical details
Menthonnex mortality improvements
The Menthonnex model smooths mortality rates across birth cohorts with a law that, in contrast to the Makeham-Gompertz model, has parameters that model the interaction of the drivers of the trend over time with age. In contrast to the Lee-Carter model, which extrapolates improvements indefinitely into the future, this model allows for the retangularisation of the mortality curve over time, and thereby implicitly assumes that the rate of decline in mortality rates will slow.
Country context for standard mortality tables
The Turkish Treasury co-ordinated a working group with Hacettepe University, Başkent University, Marmara University and BNB Consulting Firm to develop Mortality Tables, resulting in the Turkish Annuitant Life table TRHA-2010 (International Association of Actuaries, 2016[63]).
A Working Group from Hacettepe University is updating these tables to improve them and incorporate future mortality improvements.
Technical details
As there is not sufficient annuitant data from insurance companies to construct a table, all insured data is used over the period 2004-08 to construct the TRHA-2010 table. Rates for central ages are smoothed with the Whittaker Henderson model. Age specific reduction factors based on older American CSO tables are applied to these rates to result in the mortality table for annuitants (International Association of Actuaries, 2016[63]).
Country context for standard mortality tables
The Continuous Mortality Investigation (CMI) of the Institute and Faculty of Actuaries (IoFA) in the United Kingdom carries out mortality experience studies and the development of mortality tables used by pension and annuity providers. They develop a number of base mortality tables reflecting different populations. The ‘16’ Series tables are the latest able for pension annuities in payment provided by insurance companies. They are based on insurance data over the years 2015-18, including annuities purchased with pension savings as well as buy-outs. The ‘S3’ Series tables are the latest tables for self-administered pension schemes. They are based on pensioner data from 2009-16.
The CMI also makes a tool available to project future mortality improvements. The last major revision of the methodology of this model occurred in 2016. This latest model includes user inputs to control the sensitivity of the model to the most recent data, the pattern of convergence and long-term improvement rates.
Technical details
The 16 Series tables includes separate tables by internal and external buy-outs as well as tables by both lives and amounts (by gender). The central ages are graduated using the Gompertz model, and are blended to general population mortality for both younger and older ages (CMI Annuities Committee, 2020[64]).
The S3 Series includes separate tables by gender, status (all pensioner, normal health, ill health, dependent), tables based on lives or amounts, and tables based on bands of pension amounts (high, medium, and low). The graduation method used was the one most appropriate given the data, and low and high ages are blended to population mortality (CMI, 2018[65]).
The CMI projection model first smooths each year of historical rates for England and Wales across ages to follow an exponential pattern (the previous model smoothed historical rates across both years and ages using a p-spline model). An age-period-cohort improvement model is fitted to these smoothed historical rates to determine the initial rates, which are the last fitted rates of the historical period. Initial rates are interpolated to long-term rates via a function that allows users to define the weight of the most recent input data, the slope of the convergence pattern, as well as the rate of long-term improvement. Convergence periods across periods and cohorts differ, and the convergence period for younger cohorts is shorter. Long-term improvements are linearly graded down to zero between ages 85 and 110 (CMI, 2017[66]). The default settings for the 2020 version places no weight on 2020 data due to COVID-19 (CMI, 2021[67]).
Country context for standard mortality tables
The Society of Actuaries (SOA) in the United States publishes mortality tables that are used to value pension liabilities. They published the RP2014 tables in 2014 based on the mortality experience of uninsured private pension plans. The Internal Revenue Service (IRS) requires these tables to be used for minimum funding calculations and for PBGC (the pension guarantee fund) premiums. Plans are required to use these base tables in conjunction with the MP-2019 mortality improvement scale, though smaller plans commonly reduce the two-dimensional generational table to a one-dimensional static table for ease of calculations (Society of Actuaries, 2014[68]).
The SOA updated the RP2014 tables in 2019 with the Pri-2012 based on more recent mortality experience of private pension plans. They also for the first time developed a table based on the experience of public pension plans, the Pub-2010.
To accompany the RP-2014 table, the SOA produced a two-dimensional mortality scale for the first time in 2014, the MP-2014, and since then updates its projections annually. The methodology underlying the model was revised in 2018 and 2021, and the latest improvement scale issued is the MP-2021. Mortality rates are projected to converge to a long-term improvement assumption (Society of Actuaries, 2020[69]). These improvement scales are intended to be used with the base tables described above. The MP Improvement Scale was not updated for 2022, as the Committee in charge of developing the assumptions felt that it was inappropriate to include the mortality experience of 2020 in future projections without adjustment (Society of Actuaries RPEC, 2022[70]).
Separate tables are developed for annuities provide by life insurers. In 2011 the American Academy of Actuaries issued the latest annuity valuation mortality table, the IAM 2012, at the request of the National Association of Insurance Commissioners (NAIC). The table is based on the payout annuity experience of insurance companies. It is accompanied by the improvement scale G2 (American Academy of Actuaries, 2011[71]).
Technical details
The RP-2014 table is based on the mortality experience of uninsured private pension plans over the period 2004-08. Central ages are smoothed using the Whittaker-Henderson-Lowrie model. Mortality for older ages are extrapolated using the Kannisto model, subject to a cap on the mortality rate of 0.5. Mortality for younger ages are derived from the older 2008 VBT. Separate rates are developed for employees and retirees by gender are provided based on amounts rather than lives (Society of Actuaries, 2014[68]). Rates are also provided by blue and white collar, and top and bottom income quartile. A separate table was also published, the RP-2006 table, which reflects the rates at the central year of observation rather than improved to 2014.
The Pri-2012 table updates the RP-2014 table, and is based on the mortality experience of private pension plans over the period 2010-14. The same methodology was used for its construction as for the RP-2014 table, and tables are provided both by lives and amounts (Society of Actuaries, 2019[72]).
The Pub-2010 table is based on the experience of public pension plans over the period 2008-13. Its construction follows the methodology used for the RP-2014 and the Pri-2012 tables. Tables are provided for both amounts and lives, and separate tables are developed with scaling factors for employees of different sectors (teachers, public safety, general) and retirees with benefits above and below the median (Society of Actuaries, 2019[73]).
The MP-2021 Improvement Scale is based on a new model MIM-2021 introduced in 2021 and replacing RPEC_2014. It intends to allow projections that are applicable to a wider range of practice areas. It incorporates data from the National Center for Health Statistics (NCHS), which allows the model to make projections for specific socio-economic deciles based on geographical indicators. It also allows users to set intermediate rates of improvement before reaching the model-specified long-term rate of improvement. It also allows the user to adapt the basis for the initial mortality improvement rate, and make their own adjustments to account for the expected impact of COVID-19.
The MP-2021 Improvement Scale uses a 3rd order Whittaker Henderson method to smooth historical rates of the period 1950-2019, though a smoother alternative scale based on 2nd order differences is also issued. The initial improvement rate is the smoothed rate two years before the final observed year. It uses polynomial interpolation to project to a long-term improvement rate of 1.35% at age 62, which grades down linearly to 1.1% at age 80, 0.4% at age 95, and 0% at age 115. The horizontal convergence period (along ages) is 10 years and the diagonal convergence (along birth cohorts) is 20 years, with the convergence formula using a 50%/50% blending process to smooth the projected rates (Society of Actuaries, 2021[74]).
The 2012 IAM tale is based on insurance companies’ experience of immediate annuities and annuitisation and life settlement options of individual insurance policies over 2000-04. The 2012 IAR (Individual Annuity Reserving) table includes additional margins and the projection scale G2. Central mortality rates were smoothed using P-splines weighted by income amount. Rates for younger ages were derived from the 1994 GAM table projected to 2002, and the oldest ages were extrapolated using the Kannisto model. The improvement Scale G2 is set to be slightly higher than the Social Security Administration’s (SSA) projections for the public pensioners, with an additional 0.4% improvement for age 65-82, grading to 0.2% for ages 87 and over. Younger ages were assumed to improve at 1% and improvements grade to 0% for ages 105 and over (American Academy of Actuaries, 2011[71]).
Notes
← 1. The statistical institutions in most jurisdictions develop life tables for the general population, but these are not included within the scope of this chapter unless pension or annuity providers reference them in practice due to a lack of mortality tables specifically for these sectors. Nevertheless, population life tables can still a provide useful reference for the development of mortality assumptions, particularly where these tables are developed at a granular level by socio-economic groups, as is the case for example in France and the United Kingdom.
← 2. The same institutions develop the tables for pensions and insurance in Austria, Canada, Israel, Korea and the United Kingdom, whereas different institutions have developed tables for the respective sectors in Germany, Italy, Japan, Mexico, Portugal, Switzerland, and the United States.
← 3. This table is used to calculate more than half of the total technical provisions for the annuity market in Portugal.
← 4. The technical details discussed in the following sections are not always available for all jurisdictions. The examples given are often intended to demonstrate the range of approaches, but do not necessarily accurately represent how prevalent each approach is.
← 5. Life insurance here refers to the insurance product that pays benefits to beneficiaries upon the death of the policyholder.
← 6. The information included in this section refers only to the latest mortality improvement assumptions developed in each jurisdiction.
← 7. Although some may reference the population covered by the public pension system, which is generally quite close to the general population.
← 8. Some tables may also include a security margin, for example if they are used for reserving purposes, which further increases the gap in life expectancy between pensioners/annuitants and the general population.
← 9. https://avoe.at/rechnungsgrundlagen/
← 10. https://www.plan.be/databases/database_det.php?lang=nl&ID=50
← 11. https://iabe.be/expert-groups/working-groups/mortality2/overview
← 12. The information included here is based on the draft tables published for consultation. The official tables will be published in early 2023.
← 13. http://www.ressources-actuarielles.net/gtmortalite
← 14. https://www.heubeck-richttafeln.de/
← 15. Technical details of the CMI model are described in the section detailing the United Kingdom.
← 16. http://www.bvg-grundlagen.ch/franz/embargofr15122020.htm