copy the linklink copied!Chapter 4. Data and model calibration in the Auckland case study
This chapter provides a navigation of the various data sources and presents the model calibration. The first section describes the data sources, which include a travel survey conducted in New Zealand, geo-spatial data, New Zealand fleet registration data and Google API data on travel times. The chapter describes and visualises how land use and travel survey data are combined to create a stylised representation of residential and employment locations in Auckland. The second section, provides detail on the calibration of the model including the way households spend their income and allocate their time, as well as their travel behaviour and its elasticity to price and income changes. These values are important as they provide evidence of the adaptation of MOLES to Auckland and a link to the general empirical regularities reported in the literature.
copy the linklink copied!4.1. Data sources and processing
4.1.1. GIS data
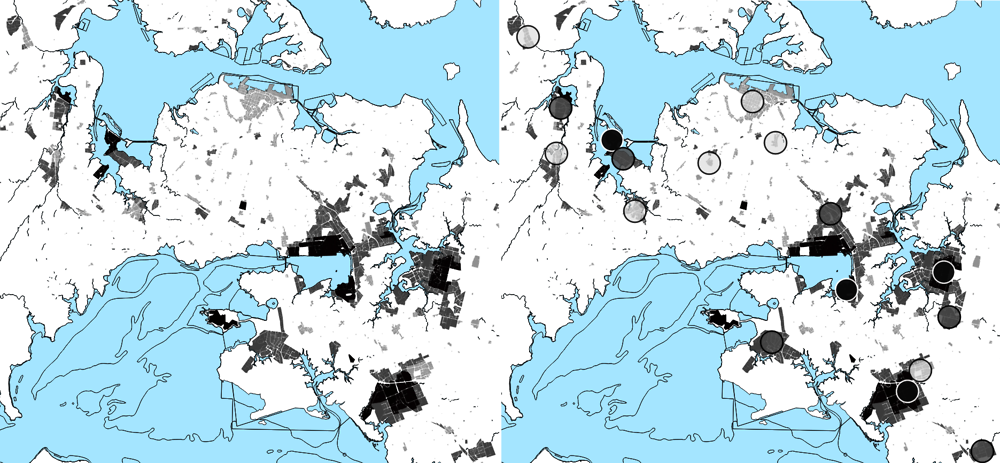
The study makes extensive use of Geographic Information System (GIS) data. The point of departure for GIS data processing is the primary parcel dataset provided by the LINZ data service (Land Information New Zealand, 2018[1]). A primary parcel is a polygon that represents a portion of land serving a single, observable land-use type from a set of 47 classes. The size of a primary parcel may vary widely, from a few square metres to surfaces exceeding a square kilometre. The upper left panel of Figure 4.1 displays a large number of primary parcels within and around Auckland’s CBD. Several primary parcels compose a meshblock (upper right panel) and several meshblocks make up an area unit (lower left panel). Meshblocks and area units are fundamental spatial delimitations at which census information is available. Finally, the lower right panel displays the model zones used in the present study. These zones are either distinct area units, or small concatenations (groups of 2-3) of them.
The land-use types that represent office spaces, light and heavy industries are used as an input in the process of constructing a satisfactory representation of the city’s employment patterns with a small set of commuting destinations, i.e. job hubs. The output of that process is shown in Figure 4.2.
The GIS data on primary land parcels are also used in order to distinguish the model zones that contain a substantial surface of residential land. Such zones could be used as residential zones in the base year of the model simulations (2018). This extraction process is shown in Figure 4.3, where all residential parcels of land are displayed together with the model zones that contain them (left panel). The right panel of the figure shows how the various concentration levels of residential land in model zones translate to a selection of model zones in which housing and land markets will be considered. Figure 4.4 displays the same exercise for the horizon year of the study. That is done by adding the land parcels that have been reserved for future residential development. The addition of these land parcels, which are shown in brown in the left panel of the picture, expands the choice of the selected model zones acting as residential locations (right panel).
Apart from being used in isolation in order to identify residential and job locations, GIS data are used in combination with data from the travel survey to identify the locations of shopping hubs and the key destinations of leisure trips.
4.1.2. Travel survey data
The study uses data from an extensive household travel survey carried out between 2003 and 2014 (New Zealand Ministry of Transport, 2018[2]). That survey covers 68 000 people from 27 000 households in New Zealand and generates information that is organized in several interrelated datasets summarised in Table 4.1. The study uses also survey data from trips conducted within Auckland. The travel survey contains information on current mobility patterns by recording representative trips from households and individuals. The records include details on the origin, destination, distance and duration of trips, the transport mode used and the household status. For the purposes of the model, the Trip (TR) dataset is linked to the Addresses (AD) dataset to obtain coordinates of the origin, destination and distance of every trip contained in the dataset.
In the initial processing stage, the trips of the travel survey were grouped according to the time and the purpose of the journey. The classification with respect to the trip’s time involved the exact same three periods that mirror the model’s temporal specification: on-peak weekday travel, off-peak weekday travel and weekend travel. Trips commencing before the start of the on-peak period but ending within it, or vice versa, were assigned to each period proportionately to the share of the trip duration falling within each of them.
Originally, trip purpose is classified in six major categories: home-returning, commuting, education, shopping, leisure and miscellaneous (i.e. trips serving any purpose other than the five listed). Home-returning trips account for 35% of reported trips. The actual purpose of home-returning trips is identified with the help of an auxiliary method. That method matches the origin of the home-returning trip to the destination of a trip undertaken earlier by the same respondent, provided that it is possible to infer the purpose of that original trip. For instance, if a respondent reported a trip to work at some point in time and a home-returning trip in the some latter time point during the same day, the two trips are matched and recorded as commuting trips.
In several instances, matching is complicated by the fact that multiple trips of different purposes are candidates to match a home-returning trip. For instance, a respondent may report a trip to a shopping mall as a shopping trip on one occasion but a leisure trip on another occasion. If the original purpose of the home-returning trip is not clear, the study assigns an equal probability to the various matching purposes. In the context of the mentioned example, this implies that the home-returning trip from this location is recorded as being 50% a shopping trip and 50% a leisure trip.
After implementing this method, more than 96% of home-returning trips were matched and reclassified as commuting, education, shopping, leisure or miscellaneous trips. Using these data manipulations results in the temporal and modal decomposition of passenger kilometres reported in Table 4.2 and Table 4.3 respectively.
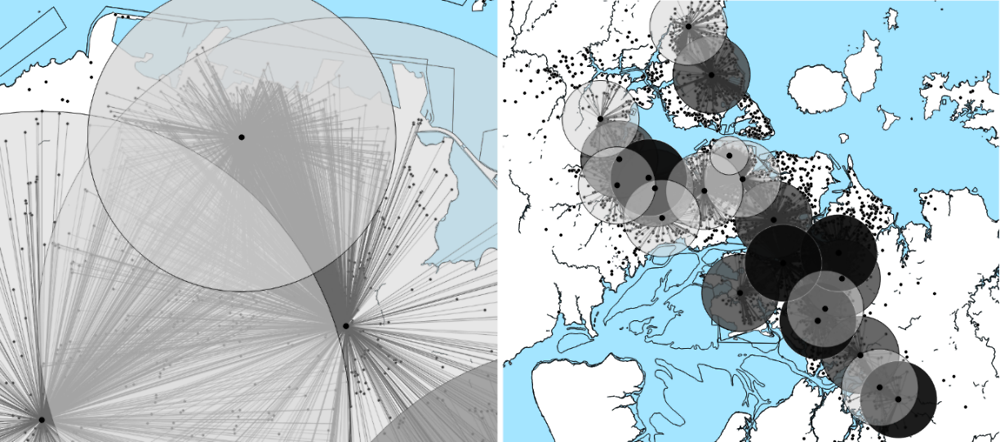
Subsequently, the commuting trips from the travel survey are geolocated (i.e. mapped) and used in combination with the GIS data. That yields a measure of the labour force’s share that is employed in each of the employment hubs. That exercise is displayed in Figure 4.5, where the destination points of the commuting trips are geolocated. The buffer zones surrounding the various employment hubs adjust in order to minimise: (i) the number of trips not being captured by any employment hub and (ii) the overlap between job hub domains of the same type (offices, light and heavy industries). This heuristic method results in a large portion of the commuting trip destination points (82%) falling within the constructed buffer zones. Many of the commuting trips the method fails to capture terminate in rural locations, reserved for agriculture. This indicates that these trips are likely to represent respondents commuting to jobs in the agricultural sector. As the agricultural sector is not modelled explicitly, these data are not used in the analysis that follows.
Due to the proximity of employment hubs of different types (e.g. a light industry hub may lie in the proximity of a heavy industry hub), a substantial overlap of two or more job hub domains is in many cases inevitable. That holds true especially in the area of the isthmus, where hubs are located close to each other. That area is displayed in the right panel of Figure 4.5. A drawback of the travel survey is that the employment type of the commuter cannot be inferred by the incorporated information. This implies that a trip destination point that belongs to the multiple buffer zones cannot be assigned with certainty to any of them. This is true even if the overlapping areas represent the domains of very different job concentrations, for example office jobs and heavy industries. To overcome this obstacle, the study uses a probabilistic method to assign a weight to each candidate job hub of a commuting trip. That weight is inversely related to the distance between the work trip destination and the employment hub. That is, the closer a job hub lies to the terminal point of a trip, the more likely it is to be the actual destination of the commuter and vice versa. Using the same weighting method, self-reported income data are linked to employment hubs in order to approximate the mean income of an employee at each employment hub.
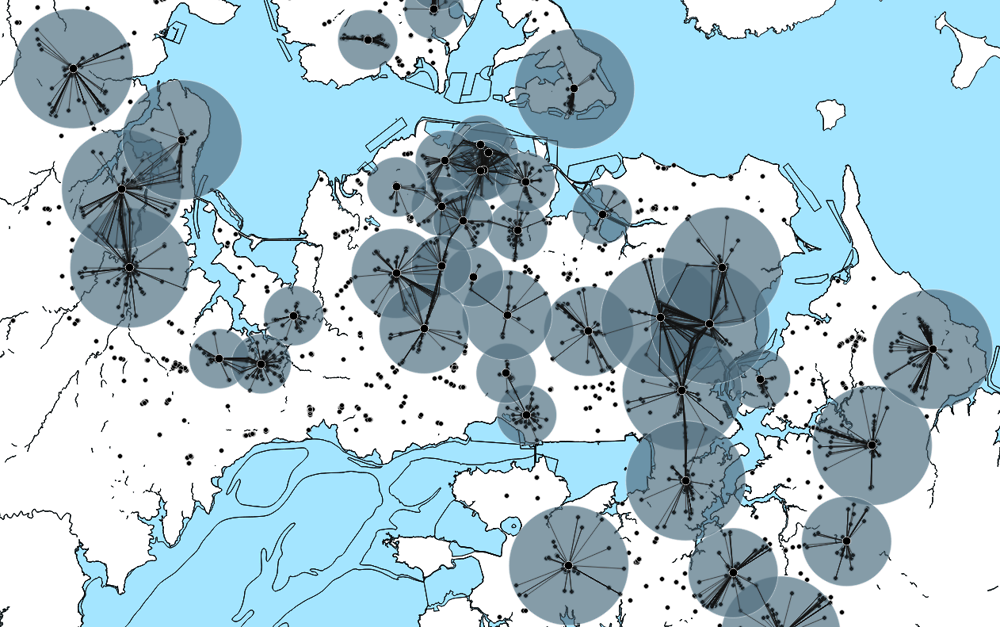
The study uses the same methodology to map shopping trips to shopping hubs. Shopping hubs are created in areas where primary land parcels of mixed use are highly concentrated. They are also directly geolocated in the case of large shopping centres. Buffer zones of various sizes are created to capture, within their domains, a satisfactory share (93.7%) of the shopping trip destinations, as shown in Figure 4.6. The same distance-weighting formula that is used to allocate commuting trips to multiple employment hubs is used to assign shopping trips to multiple candidate shopping hubs. That is, whenever the destination point of a shopping trip lies within the domain of multiple such shopping hubs, the relative proximity of that point to each hub determines the degree to which the former belongs to the latter.
Unlike the destination points of commuting and shopping trips, which display a clear spatial pattern, the respective destination points of leisure trips are scattered in a uniform manner across the entire urban fabric, as shown in the left panel of Figure 4.7. To represent leisure locations in a convenient manner, the study uses 26 points that are scattered uniformly across urban space. A fixed impact territory, i.e. buffer zone, of a three kilometre radius around these points is sufficient to capture 90.1% of leisure trip destinations.
Schooling trips are omitted from the analysis, as their contribution to the total amount of emissions is too small to justify the use of the computer-intensive methods deployed to model commuting, shopping and leisure trips. More specifically, schooling trips taken with private cars (the most carbon-intensive transport mode) make up between 1.4% and 3.6% of the total kilometres driven.1 To provide a sense of proportions, the share of commuting trips, shopping and leisure trips in total kilometres is 28.3%, 12.2% and 23.4% respectively.
4.1.3. Fuel efficiency
The average fuel economy of the New Zealand’s future fleet of conventional vehicles is among the important determinants of the study’s outcomes.2 Vehicle fuel economy is expressed as the number of kilometres driven with one litre of gasoline. Since the evolution of that variable up to 2050 is unknown, it is projected using the evolution of fuel efficiency in a sample of the Auckland’s conventional fleet from 1994 to 2018 (New Zealand Transport Agency, 2018[3]).
The evolution of the observed fuel efficiency is decomposed into a time trend and a vehicle build trend. The time trend encapsulates the overall technological progress in the automobile industry. It implies that a vehicle produced today is more fuel-efficient than a vehicle with the same observable characteristics produced in the past. The vehicle build trend implies that the average vehicle produced today has a different fuel efficiency than a vehicle produced in the past because vehicle attributes that determine fuel efficiency evolve over time. These attributes include the body type, weight, the engine type (conventional or hybrid) and capacity of the average vehicle in the fleet, as well as the market shares of the various manufacturers. The vehicle build trend captures the part of the of fuel efficiency variation that can be attributed to the fact that vehicles in a given point in time are heterogeneous: they are produced by different manufactures, weigh different amounts, have differing engine capacities and are operated in different ways. Due to this heterogeneity, vehicles produced in the same year are likely to exhibit different levels of fuel efficiency. The time trend, as well as the different trends in vehicle build extracted from the evolution of vehicle attributes, are used to extrapolate the observed fuel efficiency to the period between 2018 and 2050. The projection is based on the assumption that the multiple determinants of fuel economy will continue evolving along their in-sample trajectories.
One important driver of fuel economy evolution is the increase in the share of hybrid vehicles in the fleet. That is because hybrid vehicles are, on average, significantly more fuel-efficient than gasoline and diesel vehicles. Thus, a higher share of hybrids in the fleet improves the overall fuel economy of the fleet. To account for this aspect, the projection accounts explicitly for their share in the future fleet. More specific, it assumes that the latter share will evolve according to the current trend.
4.1.4. Other data
The model generates traffic conditions and vehicle speeds that vary across the three time intervals (on-peak, off-peak, weekends) composing a week. They also vary spatially, across the cells of the 1.8 km 1.8 km grid and across the different highway segments. In order to calibrate the model parameters that relate the levels of traffic (traffic volumes) to vehicle speeds, observations on the latter are needed. Vehicle speeds are observed with the use of Google Distance Matrix API. This database service uses accumulated observations of travel speeds and their determinants, such as day, time, season, mode of transport, and weather conditions, to predict travel time between any pair of locations.
Observations on vehicle speeds across the various grid cells are drawn separately for each of the three representative time intervals (on-peak, off-peak and weekends). The speed data collection is performed separately for privately-owned and public transport vehicles. The underlying road network is sparse in a large portion of the grid, which is represented by the set of non-coloured cells in the left panel of Figure 4.8. These are predominantly rural areas, in which the average traffic flows are low and the average speeds lie close to their free-flow levels, independent of the time of the day or the day of the week. To simplify matters, MOLES sets the speeds within those cells equal to their free-flow levels. In turn, the free-flow speeds are approximated with observations drawn from selected parts of the non-coloured part of the grid in Figure 4.8. Once these speeds are set in line with data, MOLES treats them as exogenous.
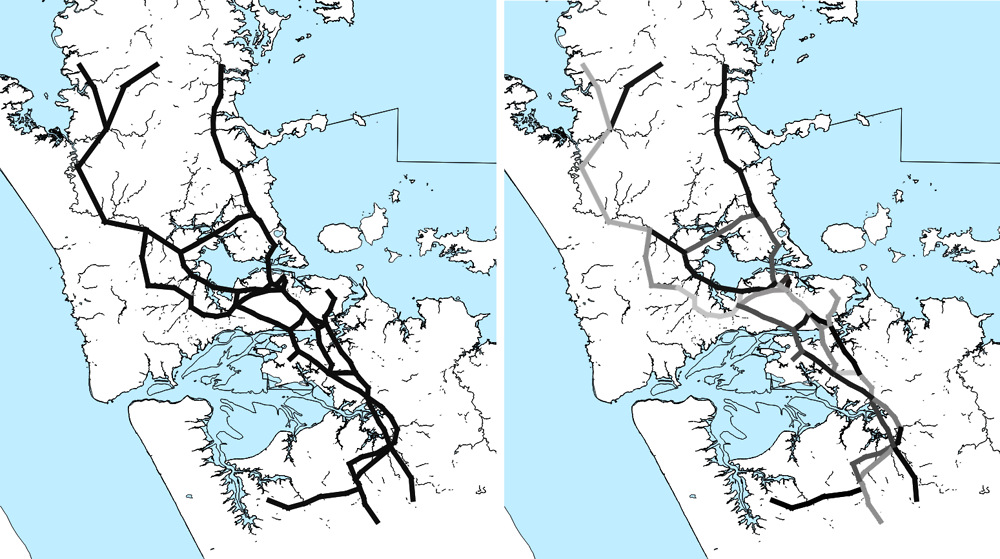
In the rest of the grid, time-averaged traffic flows are considerable and fluctuate both across cells and across the three time intervals. A large number of observations is drawn from the coloured part of the grid in Figure 4.8 to approximate the vehicle speeds with spatiotemporal accuracy. However, there is an upper bound on the distance between any pair of points within a single 1.8 km 1.8 km grid cell, which lies slightly below 2.55 km. That ceiling value sets an upper bound on the distance and travel time of the trips that are sampled to calculate the average speed in the cell. This implies that the latter is systematically underestimated, as the underlying calculations include fixed time requirements for parking or (in the case of public transport) transit. To reduce that bias, the cells are grouped into 22 groups, which are displayed in the right panel of Figure 4.8. The grouping takes into account the homogeneity of network and aims at generating well-shaped cell groups that would contain the straight-line connections between the origin and destination points drawn within them.
A similar method is used to group adjacent links in the highway network representation. The grouping of highway links is shown in the left panel of Figure 4.9.
copy the linklink copied!4.2. Model calibration
4.2.1. Population and employment densities
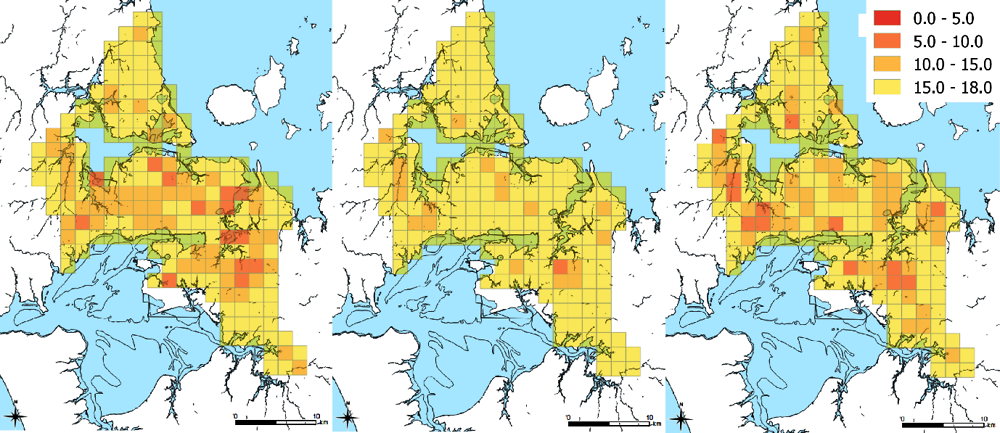
The model is calibrated in order to reproduce a series of stylised facts that characterise New Zealand and to be aligned with general empirical regularities reported in the literature. Regarding the variables determined at the local level, the model’s outcomes accord with the data processed specifically for the urban area of Auckland. The benchmark equilibrium approximates the observed population density in each model zone (left panel of Figure 4.10) and the employment density in each job hub (right panel of Figure 4.10).3
4.2.2. Income and value of time distributions
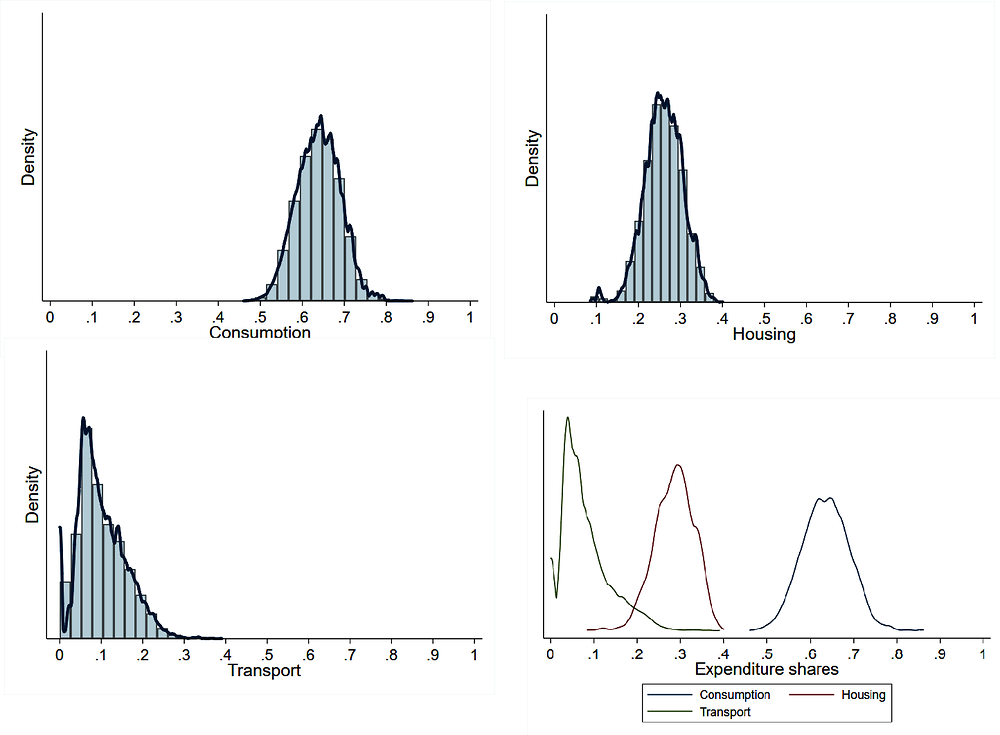
On average, 64% of the disposable income in the model is spent on consumption goods, 26% on housing and 10% on transport. These average numbers are in rough alignment with overall estimates generated by processing data from the Census. The distributions of the three expenditure shares, as predicted by the model, are displayed in Figure 4.11. Two main drivers underlie the variation in expenditure patterns predicted by the model. The first one is the spatial trade-off between transport and housing costs. That is, housing costs are higher in the most accessible locations, as jobs, shopping and leisure hubs can be reached with a relatively low pecuniary and time cost from these locations. Therefore, some individuals face relatively high housing costs and low transport costs, and vice versa. This mechanism accords with general empirical regularities and is in alignment with information obtained specifically for Auckland from a household expenditure survey. The second driver is the possibility of substitution between generic consumption and the rest of expenditure sources. For instance, individuals with high valuations of residential space will have to decrease their consumption levels in order to finance the larger housing costs they face.
Labour remuneration accounts for approximately 77% of the income generated in the simulations. The respective share of rents is 23%. The resulting net expenditure on housing is in accordance with rough estimates derived from processing the census data.
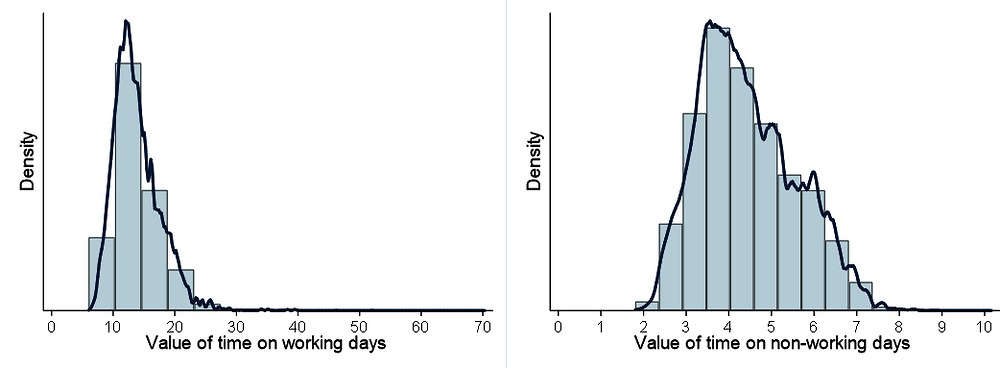
The mean value of time during a weekday is NZD 13.80 per hour. During weekends, that value falls to NZD 4.43 per hour. Both these means lie within the range of values proposed in the literature (ITF, 2017[4]). The underlying distributions of time valuation during working and non-working days are displayed in Figure 4.12. The average price elasticity of housing demand, which indicates the rigidity of residential space demand with respect to changes in housing prices, is -0.61. The associated income elasticities of housing and consumption are both unitary.4
The benchmark equilibrium yields an ownership rate (90%) that approximates the observed one. The shares of conventional and electric vehicles in the model, 99.4% and 0.6% respectively, lie close to the ones estimated from data (99.7% and 0.3%).
The travel behaviour predicted by the model fits the observations of the travel survey. That is, 77.4% of commuters use a private vehicle (85.1% in data), 13.3% use public transport (8.5% in data) and 9.3% of commuting takes place with soft mobility (6.4% in data).5
On average, an individual has a probability of 29% to make a home-based shopping trip during a weekday. If that home-based trip is realised, it most probably (96%) takes place during the off-peak hours. Home-based shopping trips occur with high probability (47.7%) during a typical weekend day. Furthermore, shopping detours can be incorporated into commuting trips. This occurs with a probability that exceeds 50% for commuting trips in weekdays and falls to 11% for the commuting trips occurring in weekend days. The vast majority of these shopping trips, 86.9%, are undertaken with a private vehicle, while a smaller portion, 13.1%, uses soft mobility. The corresponding estimates from the travel survey data are 86.5% and 13.5% respectively.
4.2.3. Vehicle speeds
Private vehicle travel speeds produced by the model were highest during off-peak periods (central panel in Figure 4.13) where vehicle speeds across the grid approached the maximum vehicle speed of 35 kilometres/hour. As expected, speeds are at their lowest level during peak periods (left panel in Figure 4.13). In those periods, the average travel speed lies between 10 and 20 kilometres per hour in areas of the network connecting the residential zones with the Central Business District (CBD). A substantial number of shopping and leisure trips taking place on weekends contribute to reduced speeds in many areas of the network (right panel in Figure 4.13).
Travelling with public transport in Auckland implies, to a large extent, the use of public buses. These use fixed routes, most of the times in the same road segments used by private cars, and make frequent stops. Therefore, the model assumes a low free-flow speed for buses (17 km/h). In many areas of the network, speed falls short of 10 kilometres per hour during the peak traffic hours on weekdays (left panel in Figure 4.14). Travel speeds are relatively higher in off-peak periods (central panel in Figure 4.14) and on weekends (left panel in Figure 4.14) but remain low in the busiest areas of the network.
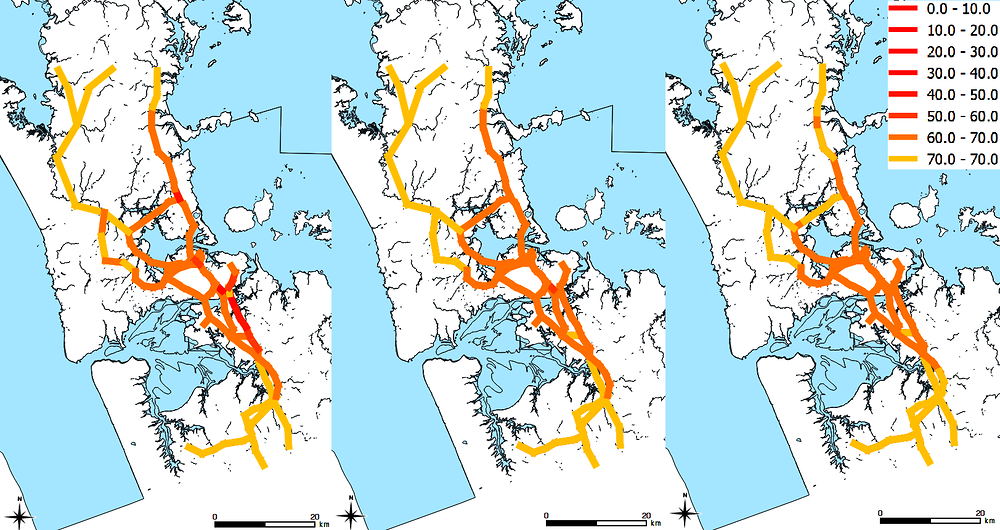
Average speeds of private vehicles on Auckland’s highway network is generally high. In many areas, speeds approach the maximum speed (i.e. the free-flow speed). That is set to of 70 km/h to account for traffic lights and any other impediment that induces a “start-stop” type of driving, even in the absence of traffic. On certain highway segments within and around the CBD, speeds fall during peak hours (left panel of Figure 4.15). In peripheral areas, speeds are close to free-flow levels during the off-peak periods of weekdays and on weekends. However, average speeds during off-peak and on weekends slow within the CBD and on highway segments leading to it from the south (central and right panel of Figure 4.15).
References
[4] ITF (2017), “Shared Mobility Simulations for Auckland”, International Transport Forum Policy Papers, No. 41, OECD Publishing, Paris, https://dx.doi.org/10.1787/5423af87-en.
[1] Land Information New Zealand (2018), LINZ data, https://www.linz.govt.nz/data/linz-data.
[2] New Zealand Ministry of Transport (2018), Household Travel Survey.
[3] New Zealand Transport Agency (2018), New Zealand vehicle fleet open data sets, https://www.nzta.govt.nz/resources/new-zealand-motor-vehicle-register-statistics/new-zealand-vehicle-fleet-open-data-sets/.
Notes
← 1. The exact number cannot be computed with certainty due to limited information on the share of trips taken by school buses in the travel survey.
← 2. Conventional cars in the study include light duty passenger cars with internal combustion or hybrid engines. The empirical work is carried out on a sample of gasoline and hybrid cars. Data on diesel cars were not of sufficient quality to be included in the econometric analysis. Instead, the evolution of the fuel economy of diesel cars is assumed to follow the trajectory as gasoline and hybrid cars do.
← 3. The average difference between of the predicted shares (population in each zone, employment in each hub) and their observed counterparts is negligible, i.e. and respectively. The corresponding standard deviations are and . The observed share of each model zone in the total population is computed by summing the population of all Auckland’s area units composing a model zone (see Figure 6.1). In turn, area unit populations were retrieved from the census. The actual employment density that corresponds to each job hub is approximated with probabilistic geospatial methods, which are described in Section 4.1.
← 4. This is an artefact of the model specification, which assumes a constant elasticity of substitution between consumption and housing.
← 5. The effect of policies on soft mobility is not analysed as the latter does not produce emissions and has zero private pecuniary costs.
Metadata, Legal and Rights
https://doi.org/10.1787/095848a3-en
© OECD 2021
The use of this work, whether digital or print, is governed by the Terms and Conditions to be found at http://www.oecd.org/termsandconditions.