3. PISA 2018 Mathematics Framework
This chapter defines “mathematical literacy” as assessed in the Programme for International Student Assessment (PISA) in 2018 and the competencies required for mathematical literacy. It explains the processes, content knowledge and contexts reflected in the tasks that PISA uses to measure scientific literacy, and how student performance in mathematics is measured and reported.
Introduction
In PISA 2018, mathematics is assessed as a minor domain, providing an opportunity to make comparisons of student performance over time. This framework continues the description and illustration of the PISA mathematics assessment as set out in the 2012 framework, when mathematics was re-examined and updated for use as the major domain in that cycle.
For PISA 2018, as in PISA 2015, the computer is the primary mode of delivery for all domains, including mathematical literacy. However, paper-based assessment instruments are provided for countries that choose not to test their students by computer. The mathematical literacy component for both the computer-based and paper-based instruments are composed of the same clusters of mathematics trend items. The number of trend items in the minor domains (of which mathematics is one in 2018) are increased, when compared to PISA assessments prior to 2015, therefore increasing the construct coverage while reducing the number of students responding to each question. This design is intended to reduce potential bias while stabilising and improving the measurement of trends.
The PISA 2018 mathematics framework is organised into several major sections. The first section, “Defining Mathematical Literacy,” explains the theoretical underpinnings of the PISA mathematics assessment, including the formal definition of the mathematical literacy construct. The second section, “Organising the Domain of Mathematics,” describes three aspects: a) the mathematical processes and the fundamental mathematical capabilities (in previous frameworks the “competencies”) underlying those processes; b) the way mathematical content knowledge is organised, and the content knowledge that is relevant to an assessment of 15-year-old students; and c) the contexts in which students face mathematical challenges. The third section, “Assessing Mathematical Literacy”, outlines the approach taken to apply the elements of the framework previously described, including the structure of the assessment, the transfer to a computer-based assessment and reporting proficiency. The 2012 framework was written under the guidance of the 2012 Mathematics Expert Group (MEG), a body appointed by the main PISA contractors with the approval of the PISA Governing Board (PGB). The ten MEG members included mathematicians, mathematics educators, and experts in assessment, technology, and education research from a range of countries. In addition, to secure more extensive input and review, a draft of the PISA 2012 mathematics framework was circulated for feedback to over 170 mathematics experts from over 40 countries. Achieve and the Australian Council for Educational Research (ACER), the two organisations contracted by the Organisation for Economic Co-operation and Development (OECD) to manage framework development, also conducted various research efforts to inform and support development work. Framework development and the PISA programme generally have been supported and informed by the ongoing work of participating countries, as in the research described in OECD (2010[1]). The PISA 2015 framework was updated under the guidance of the mathematics expert group (MEG), a body appointed by the Core 1 contractor with the approval of the PISA Governing Board (PGB). There are no substantial changes to the mathematics framework between PISA 2015 and PISA 2018.
In PISA 2012, mathematics (the major domain) was delivered as a paper-based assessment, while the computer-based assessment of mathematics (CBAM) was an optional domain that was not taken by all countries. As a result, CBAM was not part of the mathematical literacy trend. Therefore, CBAM items developed for PISA 2012 are not included in the 2015 and 2018 assessments where mathematical literacy is a minor domain, despite the change in delivery mode to computer-based.
The framework was updated for PISA 2015 to reflect the change in delivery mode, and includes a discussion of the considerations of transposing paper items to a screen and examples of what the results look like. The definition and constructs of mathematical literacy however, remain unchanged and consistent with those used in 2012.
Defining mathematical literacy
An understanding of mathematics is central to a young person’s preparedness for life in modern society. A growing proportion of problems and situations encountered in daily life, including in professional contexts, require some level of understanding of mathematics, mathematical reasoning and mathematical tools, before they can be fully understood and addressed. It is thus important to understand the degree to which young people emerging from school are adequately prepared to apply mathematics in order to understand important issues and to solve meaningful problems. An assessment at age 15 – near the end of compulsory education – provides an early indication of how individuals may respond in later life to the diverse array of situations they will encounter that involve mathematics.
The construct of mathematical literacy used in this report is intended to describe the capacities of individuals to reason mathematically and use mathematical concepts, procedures, facts and tools to describe, explain and predict phenomena. This conception of mathematical literacy supports the importance of students developing a strong understanding of concepts of pure mathematics and the benefits of being engaged in explorations in the abstract world of mathematics. The construct of mathematical literacy, as defined for PISA, strongly emphasises the need to develop students’ capacity to use mathematics in context, and it is important that they have rich experiences in their mathematics classrooms to accomplish this. In PISA 2012, mathematical literacy was defined as shown in Box 3.1. This definition is also used in the PISA 2015 and 2018 assessments.
Mathematical literacy is an individual’s capacity to formulate, employ and interpret mathematics in a variety of contexts. It includes reasoning mathematically and using mathematical concepts, procedures, facts and tools to describe, explain and predict phenomena. It assists individuals to recognise the role that mathematics plays in the world and to make the well-founded judgements and decisions needed by constructive, engaged and reflective citizens.
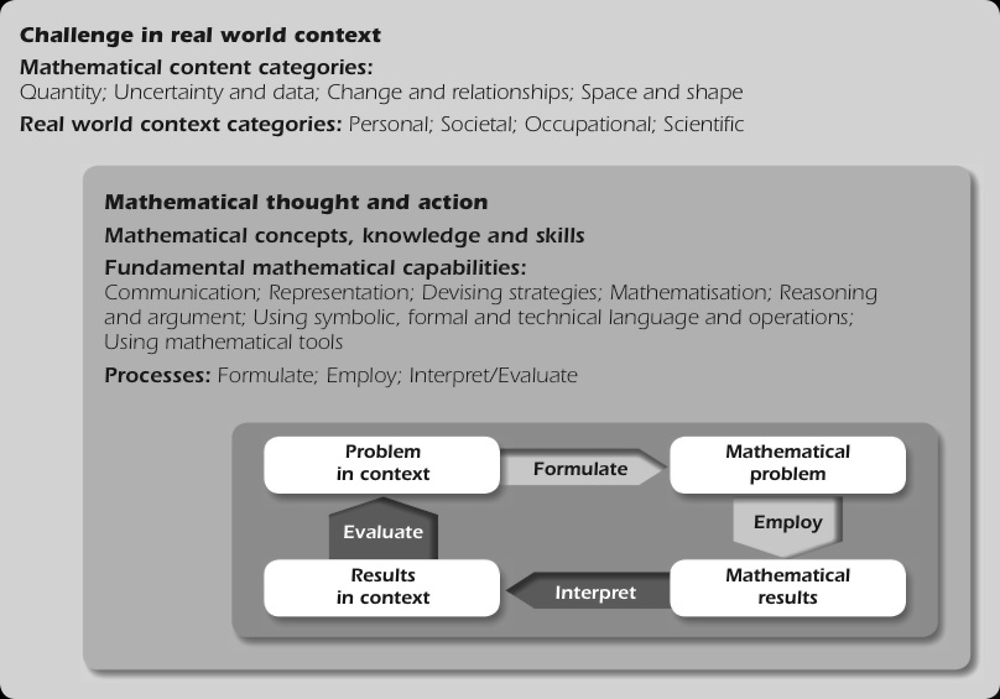
The focus of the language in the definition of mathematical literacy is on active engagement in mathematics, and is intended to encompass reasoning mathematically and using mathematical concepts, procedures, facts and tools in describing, explaining and predicting phenomena. In particular, the verbs “formulate”, “employ”, and “interpret” point to the three processes in which students as active problem solvers will engage.
The language of the definition is also intended to integrate the notion of mathematical modelling, which has historically been a cornerstone of the PISA framework for mathematics (OECD, 2004[2]), into the PISA 2012 definition of mathematical literacy. As individuals use mathematics and mathematical tools to solve problems in contexts, their work progresses through a series of stages (individually developed later in the document).
The modelling cycle is a central aspect of the PISA conception of students as active problem solvers; however, it is often not necessary to engage in every stage of the modelling cycle, especially in the context of an assessment (Blum, Galbraith and Niss, 2007, pp. 3-32[3]). The problem solver frequently carries out some steps of the modelling cycle but not all of them (e.g. when using graphs), or goes around the cycle several times to modify earlier decisions and assumptions.
The definition also acknowledges that mathematical literacy helps individuals to recognise the role that mathematics plays in the world and in helping them make the kinds of well-founded judgements and decisions required of constructive, engaged and reflective citizens.
Mathematical tools mentioned in the definition refer to a variety of physical and digital equipment, software and calculation devices. The 2015 and 2018 computer-based assessments include an online calculator as part of the test material provided for some questions.
Organising the domain of mathematics
The PISA mathematics framework defines the domain of mathematics for the PISA survey and describes an approach to assessing the mathematical literacy of 15-year-olds. That is, PISA assesses the extent to which 15-year-old students can handle mathematics adeptly when confronted with situations and problems – the majority of which are presented in real-world contexts.
For purposes of the assessment, the PISA 2012 definition of mathematical literacy – also used for the PISA 2015 and 2018 cycles – can be analysed in terms of three interrelated aspects:
-
the mathematical processes that describe what individuals do to connect the context of the problem with mathematics and thus solve the problem, and the capabilities that underlie those processes
-
the mathematical content that is targeted for use in the assessment items
-
the contexts in which the assessment items are located.
The following sections elaborate these aspects. In highlighting these aspects of the domain, the PISA 2012 mathematics framework, which is also used in PISA 2015 and PISA 2018, helps to ensure that assessment items developed for the survey reflect a range of processes, content and contexts, so that, considered as a whole, the set of assessment items effectively operationalises what this framework defines as mathematical literacy. To illustrate the aspects of mathematic literacy, examples are available in the PISA 2012 Assessment and Analytical Framework (OECD, 2013[4]) and on the PISA website (www.oecd.org/pisa/).
Several questions, based on the PISA 2012 definition of mathematical literacy, lie behind the organisation of this section of the framework. They are:
-
What processes do individuals engage in when solving contextual mathematics problems, and what capabilities do we expect individuals to be able to demonstrate as their mathematical literacy grows?
-
What mathematical content knowledge can we expect of individuals – and of 15-year-old students in particular?
-
In what contexts can mathematical literacy be observed and assessed?
Mathematical processes and the underlying mathematical capabilities
Mathematical processes
The definition of mathematical literacy refers to an individual’s capacity to formulate, employ and interpret mathematics. These three words – formulate, employ and interpret – provide a useful and meaningful structure for organising the mathematical processes that describe what individuals do to connect the context of a problem with the mathematics and thus solve the problem. Items in the PISA 2018 mathematics assessment are assigned to one of three mathematical processes:
-
formulating situations mathematically
-
employing mathematical concepts, facts, procedures and reasoning
-
interpreting, applying and evaluating mathematical outcomes.
It is important for both policy makers and those involved more closely in the day-to-day education of students to know how effectively students are able to engage in each of these processes. The formulating process indicates how effectively students are able to recognise and identify opportunities to use mathematics in problem situations and then provide the necessary mathematical structure needed to formulate that contextualised problem into a mathematical form. The employing process indicates how well students are able to perform computations and manipulations and apply the concepts and facts that they know to arrive at a mathematical solution to a problem formulated mathematically. The interpreting process indicates how effectively students are able to reflect upon mathematical solutions or conclusions, interpret them in the context of a real-world problem, and determine whether the results or conclusions are reasonable. Students’ facility in applying mathematics to problems and situations is dependent on skills inherent in all three of these processes, and an understanding of their effectiveness in each category can help inform both policy-level discussions and decisions being made closer to the classroom level.
Formulating situations mathematically
The word formulate in the definition of mathematical literacy refers to individuals being able to recognise and identify opportunities to use mathematics and then provide mathematical structure to a problem presented in some contextualised form. In the process of formulating situations mathematically, individuals determine where they can extract the essential mathematics to analyse, set up and solve the problem. They translate from a real-world setting to the domain of mathematics and provide the real-world problem with mathematical structure, representations and specificity. They reason about and make sense of constraints and assumptions in the problem. Specifically, this process of formulating situations mathematically includes activities such as the following:
-
identifying the mathematical aspects of a problem situated in a real-world context and identifying the significant variables
-
recognising mathematical structure (including regularities, relationships and patterns) in problems or situations
-
simplifying a situation or problem in order to make it amenable to mathematical analysis
-
identifying constraints and assumptions behind any mathematical modelling and simplifications gleaned from the context
-
representing a situation mathematically, using appropriate variables, symbols, diagrams and standard models
-
representing a problem in a different way, including organising it according to mathematical concepts and making appropriate assumptions
-
understanding and explaining the relationships between the context-specific language of a problem and the symbolic and formal language needed to represent it mathematically
-
translating a problem into mathematical language or a representation
-
recognising aspects of a problem that correspond with known problems or mathematical concepts, facts or procedures
-
using technology (such as a spreadsheet or the list facility on a graphing calculator) to portray a mathematical relationship inherent in a contextualised problem.
Employing mathematical concepts, facts, procedures and reasoning
The word employ in the definition of mathematical literacy refers to individuals being able to apply mathematical concepts, facts, procedures and reasoning to solve mathematically formulated problems to obtain mathematical conclusions. In the process of employing mathematical concepts, facts, procedures and reasoning to solve problems, individuals perform the mathematical procedures needed to derive results and find a mathematical solution (e.g. performing arithmetic computations, solving equations, making logical deductions from mathematical assumptions, performing symbolic manipulations, extracting mathematical information from tables and graphs, representing and manipulating shapes in space, and analysing data). They work on a model of the problem situation, establish regularities, identify connections between mathematical entities, and create mathematical arguments. Specifically, this process of employing mathematical concepts, facts, procedures and reasoning includes activities such as:
-
devising and implementing strategies for finding mathematical solutions
-
using mathematical tools1, including technology, to help find exact or approximate solutions
-
applying mathematical facts, rules, algorithms and structures when finding solutions
-
manipulating numbers, graphical and statistical data and information, algebraic expressions and equations, and geometric representations
-
making mathematical diagrams, graphs and constructions, and extracting mathematical information from them
-
using and switching between different representations in the process of finding solutions
-
making generalisations based on the results of applying mathematical procedures to find solutions
-
reflecting on mathematical arguments and explaining and justifying mathematical results.
Interpreting, applying and evaluating mathematical outcomes
The word interpret used in the definition of mathematical literacy focuses on the abilities of individuals to reflect upon mathematical solutions, results, or conclusions and interpret them in the context of real-life problems. This involves translating mathematical solutions or reasoning back into the context of a problem and determining whether the results are reasonable and make sense in the context of the problem. This mathematical process category encompasses both the “interpret” and “evaluate” arrows noted in the previously defined model of mathematical literacy in practice (see Figure 3.1). Individuals engaged in this process may be called upon to construct and communicate explanations and arguments in the context of the problem, reflecting on both the modelling process and its results. Specifically, this process of interpreting, applying and evaluating mathematical outcomes includes activities such as:
-
interpreting a mathematical result back into the real-world context
-
evaluating the reasonableness of a mathematical solution in the context of a real-world problem
-
understanding how the real world impacts the outcomes and calculations of a mathematical procedure or model in order to make contextual judgements about how the results should be adjusted or applied
-
explaining why a mathematical result or conclusion does, or does not, make sense given the context of a problem
-
understanding the extent and limits of mathematical concepts and mathematical solutions
-
critiquing and identifying the limits of the model used to solve a problem.
Desired distribution of items by mathematical process
The goal in constructing the assessment is to achieve a balance that provides approximately equal weighting between the two processes that involve making a connection between the real world and the mathematical world and the process that calls for students to be able to work on a mathematically formulated problem. Table 3.1 shows the desired distribution of items by process.
Fundamental mathematical capabilities underlying the mathematical processes
A decade of experience in developing PISA items and analysing the ways in which students respond to items has revealed that there is a set of fundamental mathematical capabilities that underpins each of these reported processes and mathematical literacy in practice. The work of Mogens Niss and his Danish colleagues (Niss, 2003[5]; Niss and Jensen, 2002[6]; Niss and Højgaard, 2011[7]) identified eight capabilities – referred to as “competencies” by Niss and in the PISA 2003 framework (OECD, 2004[2]) – that are instrumental to mathematical behaviour.
The PISA 2018 framework uses a modified formulation of this set of capabilities, which condenses the number from eight to seven based on an investigation of the operation of the competencies through previously administered PISA items (Turner et al., 2013[8]). These cognitive capabilities are available to or learnable by individuals in order to understand and engage with the world in a mathematical way, or to solve problems. As the level of mathematical literacy possessed by an individual increases, that individual is able to draw to an increasing degree on the fundamental mathematical capabilities (Turner and Adams, 2012[9]). Thus, increasing activation of fundamental mathematical capabilities is associated with increasing item difficulty. This observation has been used as the basis of the descriptions of different proficiency levels of mathematical literacy reported in previous PISA surveys and discussed later in this framework.
The seven fundamental mathematical capabilities used in this framework are as follows:
-
Communication: Mathematical literacy involves communication. The individual perceives the existence of some challenge and is stimulated to recognise and understand a problem situation. Reading, decoding and interpreting statements, questions, tasks or objects enables the individual to form a mental model of the situation, which is an important step in understanding, clarifying and formulating a problem. During the solution process, intermediate results may need to be summarised and presented. Later on, once a solution has been found, the problem solver may need to present the solution, and perhaps an explanation or justification, to others.
-
Mathematising: Mathematical literacy can involve transforming a problem defined in the real world to a strictly mathematical form (which can include structuring, conceptualising, making assumptions, and/or formulating a model), or interpreting or evaluating a mathematical outcome or a mathematical model in relation to the original problem. The term mathematising is used to describe the fundamental mathematical activities involved.
-
Representation: Mathematical literacy frequently involves representations of mathematical objects and situations. This can entail selecting, interpreting, translating between, and using a variety of representations to capture a situation, interact with a problem, or to present one’s work. The representations referred to include graphs, tables, diagrams, pictures, equations, formulae and concrete materials.
-
Reasoning and argument: This capability involves logically rooted thought processes that explore and link problem elements so as to make inferences from them, check a justification that is given, or provide a justification of statements or solutions to problems.
-
Devising strategies for solving problems: Mathematical literacy frequently requires devising strategies for solving problems mathematically. This involves a set of critical control processes that guide an individual to effectively recognise, formulate and solve problems. This skill is characterised as selecting or devising a plan or strategy to use mathematics to solve problems arising from a task or context, as well as guiding its implementation. This mathematical capability can be demanded at any of the stages of the problem-solving process.
-
Using symbolic, formal and technical language and operations: Mathematical literacy requires using symbolic, formal and technical language and operations. This involves understanding, interpreting, manipulating, and making use of symbolic expressions within a mathematical context (including arithmetic expressions and operations) governed by mathematical conventions and rules. It also involves understanding and utilising formal constructs based on definitions, rules and formal systems and also using algorithms with these entities. The symbols, rules and systems used vary according to what particular mathematical content knowledge is needed for a specific task to formulate, solve or interpret the mathematics.
-
Using mathematical tools1: Mathematical tools include physical tools, such as measuring instruments, as well as calculators and computer-based tools that are becoming more widely available. In addition to knowing how to use these tools to assist them in completing mathematical tasks, students need to know about the limitations of such tools. Mathematical tools can also have an important role in communicating results.
These capabilities are evident to varying degrees in each of the three mathematical processes. The ways in which these capabilities manifest themselves within the three processes are described in Figure 3.1.
A good guide to the empirical difficulty of items can be obtained by considering which aspects of the fundamental mathematical capabilities are required for planning and executing a solution (Turner and Adams, 2012[9]; Turner et al., 2013[8]). The easiest items will require the activation of few capabilities and in a relatively straightforward way. The hardest items require complex activation of several capabilities. Predicting difficulty requires consideration of both the number of capabilities and the complexity of activation required.
Mathematical content knowledge
An understanding of mathematical content – and the ability to apply that knowledge to the solution of meaningful contextualised problems – is important for citizens in the modern world. That is, to solve problems and interpret situations in personal, occupational, societal and scientific contexts, there is a need to draw upon certain mathematical knowledge and understandings.
Mathematical structures have been developed over time as a means to understand and interpret natural and social phenomena. In schools, the mathematics curriculum is typically organised around content strands (e.g. number, algebra and geometry) and detailed topic lists that reflect historically well-established branches of mathematics and that help in defining a structured curriculum. However, outside the mathematics classroom, a challenge or situation that arises is usually not accompanied by a set of rules and prescriptions that shows how the challenge can be met. Rather, it typically requires some creative thought in seeing the possibilities of bringing mathematics to bear on the situation and in formulating it mathematically. Often a situation can be addressed in different ways drawing on different mathematical concepts, procedures, facts or tools.
Since the goal of PISA is to assess mathematical literacy, an organisational structure for mathematical content knowledge is proposed based on the mathematical phenomena that underlie broad classes of problems and which have motivated the development of specific mathematical concepts and procedures. Because national mathematics curricula are typically designed to equip students with knowledge and skills that address these same underlying mathematical phenomena, the outcome is that the range of content arising from organising content this way is closely aligned with that typically found in national mathematics curricula. This framework lists some content topics appropriate for assessing the mathematical literacy of 15-year-old students, based on analyses of national standards from eleven countries.
To organise the domain of mathematics for purposes of assessing mathematical literacy, it is important to select a structure that grows out of historical developments in mathematics, that encompasses sufficient variety and depth to reveal the essentials of mathematics, and that also represents, or includes, the conventional mathematical strands in an acceptable way. Thus, a set of content categories that reflects the range of underlying mathematical phenomena was selected for the PISA 2018 framework, consistent with the categories used for previous PISA surveys.
The following list of content categories, therefore, is used in PISA 2018 to meet the requirements of historical development, coverage of the domain of mathematics and the underlying phenomena which motivate its development, and reflection of the major strands of school curricula. These four categories characterise the range of mathematical content that is central to the discipline and illustrate the broad areas of content used in the test items for PISA 2018:
-
Change and relationships
-
Space and shape
-
Quantity
-
Uncertainty and data
With these four categories, the mathematical domain can be organised in a way that ensures a spread of items across the domain and focuses on important mathematical phenomena, but at the same time, avoids a too fine division that would work against a focus on rich and challenging mathematical problems based on real situations. While categorisation by content category is important for item development and selection, and for reporting of assessment results, it is important to note that some specific content topics may materialise in more than one content category. Connections between aspects of content that span these four content categories contribute to the coherence of mathematics as a discipline and are apparent in some of the assessment items for the PISA 2018 assessment.
The broad mathematical content categories and the more specific content topics appropriate for 15-year-old students described later in this section reflect the level and breadth of content that is eligible for inclusion on the PISA 2018 assessment. Narrative descriptions of each content category and the relevance of each to solving meaningful problems are provided first, followed by more specific definitions of the kinds of content that are appropriate for inclusion in an assessment of mathematical literacy of 15-year-old students. These specific topics reflect commonalities found in the expectations set by a range of countries and education jurisdictions. The standards examined to identify these content topics are viewed as evidence not only of what is taught in mathematics classrooms in these countries but also as indicators of what countries view as important knowledge and skills for preparing students of this age to become constructive, engaged and reflective citizens.
Descriptions of the mathematical content knowledge that characterise each of the four categories – change and relationships, space and shape, quantity, and uncertainty and data – are provided below.
Change and relationships
The natural and designed worlds display a multitude of temporary and permanent relationships among objects and circumstances, where changes occur within systems of inter-related objects or in circumstances where the elements influence one another. In many cases, these changes occur over time, and in other cases changes in one object or quantity are related to changes in another. Some of these situations involve discrete change; others change continuously. Some relationships are of a permanent, or invariant, nature. Being more literate about change and relationships involves understanding fundamental types of change and recognising when they occur in order to use suitable mathematical models to describe and predict change. Mathematically this means modelling the change and the relationships with appropriate functions and equations, as well as creating, interpreting, and translating among symbolic and graphical representations of relationships.
Change and relationships is evident in such diverse settings as growth of organisms, music, and the cycle of seasons, weather patterns, employment levels and economic conditions. Aspects of the traditional mathematical content of functions and algebra, including algebraic expressions, equations and inequalities, tabular and graphical representations, are central in describing, modelling and interpreting change phenomena. Representations of data and relationships described using statistics also are often used to portray and interpret change and relationships, and a firm grounding in the basics of number and units is also essential to defining and interpreting change and relationships. Some interesting relationships arise from geometric measurement, such as the way that changes in perimeter of a family of shapes might relate to changes in area, or the relationships among lengths of the sides of triangles.
Space and shape
Space and shape encompasses a wide range of phenomena that are encountered everywhere in our visual and physical world: patterns, properties of objects, positions and orientations, representations of objects, decoding and encoding of visual information, navigation and dynamic interaction with real shapes as well as with representations. Geometry serves as an essential foundation for space and shape, but the category extends beyond traditional geometry in content, meaning and method, drawing on elements of other mathematical areas such as spatial visualisation, measurement and algebra. For instance, shapes can change, and a point can move along a locus, thus requiring function concepts. Measurement formulas are central in this area. The manipulation and interpretation of shapes in settings that call for tools ranging from dynamic geometry software to Global Positioning System (GPS) software are included in this content category.
PISA assumes that the understanding of a set of core concepts and skills is important to mathematical literacy relative to space and shape. Mathematical literacy in the area of space and shape involves a range of activities such as understanding perspective (for example in paintings), creating and reading maps, transforming shapes with and without technology, interpreting views of three-dimensional scenes from various perspectives and constructing representations of shapes.
Quantity
The notion of Quantity may be the most pervasive and essential mathematical aspect of engaging with, and functioning in, our world. It incorporates the quantification of attributes of objects, relationships, situations and entities in the world, understanding various representations of those quantifications, and judging interpretations and arguments based on quantity. To engage with the quantification of the world involves understanding measurements, counts, magnitudes, units, indicators, relative size, and numerical trends and patterns. Aspects of quantitative reasoning – such as number sense, multiple representations of numbers, elegance in computation, mental calculation, estimation and assessment of reasonableness of results – are the essence of mathematical literacy relative to quantity.
Quantification is a primary method for describing and measuring a vast set of attributes of aspects of the world. It allows for the modelling of situations, for the examination of change and relationships, for the description and manipulation of space and shape, for organising and interpreting data, and for the measurement and assessment of uncertainty. Thus mathematical literacy in the area of quantity applies knowledge of number and number operations in a wide variety of settings.
Uncertainty and data
In science, technology and everyday life, uncertainty is a given. Uncertainty is therefore a phenomenon at the heart of the mathematical analysis of many problem situations, and the theory of probability and statistics as well as techniques of data representation and description have been established to deal with it. The uncertainty and data content category includes recognising the place of variation in processes, having a sense of the quantification of that variation, acknowledging uncertainty and error in measurement, and knowing about chance. It also includes forming, interpreting and evaluating conclusions drawn in situations where uncertainty is central. The presentation and interpretation of data are key concepts in this category (Moore, 1997[10]).
There is uncertainty in scientific predictions, poll results, weather forecasts and economic models. There is variation in manufacturing processes, test scores and survey findings, and chance is fundamental to many recreational activities enjoyed by individuals. The traditional curricular areas of probability and statistics provide formal means of describing, modelling and interpreting a certain class of uncertainty phenomena, and for making inferences. In addition, knowledge of number and of aspects of algebra, such as graphs and symbolic representation, contribute to facility in engaging in problems in this content category. The focus on the interpretation and presentation of data is an important aspect of the uncertainty and data category.
Desired distribution of items by content category
The trend items selected for PISA 2015 and 2018 are distributed across the four content categories, as shown in Table 3.3. The goal in constructing the assessment is a balanced distribution of items with respect to content category, since all of these domains are important for constructive, engaged and reflective citizens.
Content topics for guiding the assessment of mathematical literacy
To effectively understand and solve contextualised problems involving change and relationships, space and shape, quantity and uncertainty and data requires drawing upon a variety of mathematical concepts, procedures, facts, and tools at an appropriate level of depth and sophistication. As an assessment of mathematical literacy, PISA strives to assess the levels and types of mathematics that are appropriate for 15-year-old students on a trajectory to become constructive, engaged and reflective citizens able to make well-founded judgements and decisions. It is also the case that PISA, while not designed or intended to be a curriculum-driven assessment, strives to reflect the mathematics that students have likely had the opportunity to learn by the time they are 15 years old.
The content included in PISA 2018 is the same as that developed in PISA 2012. The four content categories of change and relationships, space and shape, quantity and uncertainty and data serve as the foundation for identifying this range of content, yet there is not a one-to-one mapping of content topics to these categories. The following content is intended to reflect the centrality of many of these concepts to all four content categories and reinforce the coherence of mathematics as a discipline. It intends to be illustrative of the content topics included in PISA 2018, rather than an exhaustive listing:
-
Functions: the concept of function, emphasising but not limited to linear functions, their properties, and a variety of descriptions and representations of them. Commonly used representations are verbal, symbolic, tabular and graphical.
-
Algebraic expressions: verbal interpretation of and manipulation with algebraic expressions, involving numbers, symbols, arithmetic operations, powers and simple roots.
-
Equations and inequalities: linear and related equations and inequalities, simple second-degree equations, and analytic and non-analytic solution methods.
-
Co-ordinate systems: representation and description of data, position and relationships.
-
Relationships within and among geometrical objects in two and three dimensions: static relationships such as algebraic connections among elements of figures (e.g. the Pythagorean theorem as defining the relationship between the lengths of the sides of a right triangle), relative position, similarity and congruence, and dynamic relationships involving transformation and motion of objects, as well as correspondences between two- and three-dimensional objects.
-
Measurement: quantification of features of and among shapes and objects, such as angle measures, distance, length, perimeter, circumference, area and volume.
-
Numbers and units: concepts, representations of numbers and number systems, including properties of integer and rational numbers, relevant aspects of irrational numbers, as well as quantities and units referring to phenomena such as time, money, weight, temperature, distance, area and volume, and derived quantities and their numerical description.
-
Arithmetic operations: the nature and properties of these operations and related notational conventions.
-
Percents, ratios and proportions: numerical description of relative magnitude and the application of proportions and proportional reasoning to solve problems.
-
Counting principles: simple combinations and permutations.
-
Estimation: purpose-driven approximation of quantities and numerical expressions, including significant digits and rounding.
-
Data collection, representation and interpretation: nature, genesis and collection of various types of data, and the different ways to represent and interpret them.
-
Data variability and its description: concepts such as variability, distribution and central tendency of data sets, and ways to describe and interpret these in quantitative terms.
-
Samples and sampling: concepts of sampling and sampling from data populations, including simple inferences based on properties of samples.
-
Chance and probability: notion of random events, random variation and its representation, chance and frequency of events, and basic aspects of the concept of probability.
Contexts
The choice of appropriate mathematical strategies and representations is often dependent on the context in which a mathematics problem arises. Context is widely regarded as an aspect of problem solving that imposes additional demands on the problem solver (see (Watson and Callingham, 2003[11]) for findings about statistics). It is important that a wide variety of contexts is used in the PISA assessment. This offers the possibility of connecting with the broadest possible range of individual interests and with the range of situations in which individuals operate in the 21st century.
For purposes of the PISA 2018 mathematics framework, four context categories have been defined and are used to classify assessment items developed for the PISA survey:
-
Personal – Problems classified in the personal context category focus on activities of one’s self, one’s family or one’s peer group. The kinds of contexts that may be considered personal include (but are not limited to) those involving food preparation, shopping, games, personal health, personal transportation, sports, travel, personal scheduling and personal finance.
-
Occupational – Problems classified in the occupational context category are centred on the world of work. Items categorised as occupational may involve (but are not limited to) such things as measuring, costing and ordering materials for building, payroll/accounting, quality control, scheduling/inventory, design/architecture and job-related decision making. Occupational contexts may relate to any level of the workforce, from unskilled work to the highest levels of professional work, although items in the PISA assessment must be accessible to 15-year-old students.
-
Societal – Problems classified in the societal context category focus on one’s community (whether local, national or global). They may involve (but are not limited to) such things as voting systems, public transport, government, public policies, demographics, advertising, national statistics and economics. Although individuals are involved in all of these things in a personal way, in the societal context category the focus of problems is on the community perspective.
-
Scientific – Problems classified in the scientific category relate to the application of mathematics to the natural world and issues and topics related to science and technology. Particular contexts might include (but are not limited to) such areas as weather or climate, ecology, medicine, space science, genetics, measurement and the world of mathematics itself. Items that are intra-mathematical, where all the elements involved belong in the world of mathematics, fall within the scientific context.
PISA assessment items are arranged in units that share stimulus material. It is therefore usually the case that all items in the same unit belong to the same context category. Exceptions do arise; for example stimulus material may be examined from a personal point of view in one item and a societal point of view in another. When an item involves only mathematical constructs without reference to the contextual elements of the unit within which it is located, it is allocated to the context category of the unit. In the unusual case of a unit involving only mathematical constructs and being without reference to any context outside of mathematics, the unit is assigned to the scientific context category.
Using these context categories provides the basis for selecting a mix of item contexts and ensures that the assessment reflects a broad range of uses of mathematics, ranging from everyday personal uses to the scientific demands of global problems. Moreover, it is important that each context category be populated with assessment items having a broad range of item difficulties. Given that the major purpose of these context categories is to challenge students in a broad range of problem contexts, each category should contribute substantially to the measurement of mathematical literacy. It should not be the case that the difficulty level of assessment items representing one context category is systematically higher or lower than the difficulty level of assessment items in another category.
In identifying contexts that may be relevant, it is critical to keep in mind that a purpose of the assessment is to gauge the use of mathematical content knowledge, processes and capabilities that students have acquired by the age of 15. Contexts for assessment items, therefore, are selected in light of relevance to students’ interests and lives, and the demands that will be placed upon them as they enter society as constructive, engaged and reflective citizens. National project managers from countries participating in the PISA survey are involved in judging the degree of such relevance.
Desired distribution of items by context category
The trend items selected for the PISA 2015 and 2018 mathematics assessment represent a spread across these context categories, as described in Table 3.4. With this balanced distribution, no single context type is allowed to dominate, providing students with items that span a broad range of individual interests and a range of situations that they might expect to encounter in their lives.
Assessing mathematical literacy
This section outlines the approach taken to apply the elements of the framework described in previous sections to PISA 2015. This includes the structure of the mathematics component of the PISA survey, arrangements for transferring the paper-based trend items to a computer-based delivery, and reporting mathematical proficiency.
Structure of the survey instrument
In 2012, when mathematical literacy was the major domain, the paper-based instrument contained a total of 270 minutes of mathematics material. The material was arranged in nine clusters of items, with each cluster representing 30 minutes of testing time. The item clusters were placed in test booklets according to a rotated design, they also contained linked materials.
Mathematical literacy is a minor domain in 2018 and students are asked to complete fewer clusters. However the item clusters are similarly constructed and rotated. Six mathematics clusters from previous cycles, including one “easy” and one “hard”, are used in one of three designs, depending on whether countries take the Collaborative Problem Solving option or not, or whether they take the test on paper. Using six clusters rather than three as was customary for the minor domains in previous cycles results in a larger number of trend items, therefore the construct coverage is increased. However, the number of students responding to each question is lower. This design is intended to reduce potential bias, thus stabilising and improving the measurement of trends. The field trial was used to perform a mode-effect study and to establish equivalence between the computer- and paper-based forms.
Response formats
Three types of response format are used to assess mathematical literacy in PISA 2018: open constructed-response, closed constructed-response and selected-response (simple and complex multiple-choice) items. Open constructed-response items require a somewhat extended written response from a student. Such items also may ask the student to show the steps taken or to explain how the answer was reached. These items require trained experts to manually code student responses.
Closed constructed-response items provide a more structured setting for presenting problem solutions, and they produce a student response that can be easily judged to be either correct or incorrect. Often student responses to questions of this type can be keyed into data-capture software, and coded automatically, but some must be manually coded by trained experts. The most frequent closed constructed-responses are single numbers.
Selected- response items require students to choose one or more responses from a number of response options. Responses to these questions can usually be automatically processed. About equal numbers of each of these response formats is used to construct the survey instruments.
Item scoring
Although most of the items are dichotomously scored (that is, responses are awarded either credit or no credit), the open constructed-response items can sometimes involve partial credit scoring, which allows responses to be assigned credit according to differing degrees of “correctness” of responses. For each such item, a detailed coding guide that allows for full credit, partial credit or no credit is provided to persons trained in the coding of student responses across the range of participating countries to ensure coding of responses is done in a consistent and reliable way. To maximise the comparability between the paper-based and computer-based assessments, careful attention is given to the scoring guides in order to ensure that the important elements are included.
Computer-based assessment of mathematics
The main mode of delivery for the PISA 2012 assessment was paper-based. In moving to computer-based delivery for 2015, care was taken to maximise comparability between the two assessments. The following section describes some of the features intrinsic to a computer-based assessment. Although these features provide the opportunities outlined below, to ensure comparability the PISA 2015 and 2018 assessments consist solely of items from the 2012 paper-based assessment. The features described here, however, will be used in future PISA assessments when their introduction can be controlled to ensure comparability with prior assessments.
Increasingly, mathematics tasks at work involve some kind of electronic technology, so that mathematical literacy and computer use are melded together (Hoyles et al., 2002[12]). For employees at all levels of the workplace, there is now an interdependency between mathematical literacy and the use of computer technology. Solving PISA items on a computer rather than on paper moves PISA into the reality and the demands of the 21st century.
There is a great deal of research evidence into paper- and computer-based test performance, but findings are mixed. Some research suggests that a computer-based testing environment can influence students’ performance. Richardson et al. (2002[13]) reported that students found computer-based problem-solving tasks engaging and motivating, often despite the unfamiliarity of the problem types and the challenging nature of the items. They were sometimes distracted by attractive graphics, and sometime used poor heuristics when attempting tasks.
In one of the largest comparisons of paper-based and computer-based testing, Sandene et al. (2005[14]) found that eighth-grade students’ mean score was four points higher on a computer-based mathematics test than on an equivalent paper-based test. Bennett et al. (2008[15]) concluded from his research that computer familiarity affects performance on computer-based mathematics tests, while others have found that the range of functions available through computer-based tests can affect performance. For example, Mason (Mason, Patry and Bernstein, 2001[16]) found that students’ performance was negatively affected in computer-based tests compared to paper-based tests when there was no opportunity on the computer version to review and check responses. Bennett (2003[17]) found that screen size affected scores on verbal-reasoning tests, possibly because smaller computer screens require scrolling.
By contrast, Wang et al. (Wang et al., 2007[18]) conducted a meta-analysis of studies pertaining to K-12 students’ mathematics achievements which indicated that administration mode has no statistically significant effect on scores. Moreover, recent mode studies that were part of the Programme for the International Assessment of Adult Competencies (PIAAC) suggested that equality can be achieved (OECD, 2014[19]). In this study, adults were randomly assigned to either a computer-based or paper-based assessment of literacy and numeracy skills. The majority of the items used in the paper delivery mode were adapted for computer delivery and used in this study. Analyses of these data revealed that almost all of the item parameters were stable across the two modes, thus demonstrating the ability to place respondents on the same literacy and numeracy scale. Given this, it is hypothesised that mathematics items used in PISA 2012 can be transposed onto a screen without affecting trend data. The PISA 2015 field trial studied the effect on student performance of the change in mode of delivery; for further details see Annex A6 of PISA 2015 Results, Volume I (OECD, 2016[20]).
Just as paper-based assessments rely on a set of fundamental skills for working with printed materials, computer-based assessments rely on a set of fundamental information and communications technology (ICT) skills for using computers. These include knowledge of basic hardware (e.g. keyboard and mouse) and basic conventions (e.g. arrows to move forward and specific buttons to press to execute commands). The intention is to keep such skills to a minimal, core level in the computer-based assessment.
Reporting proficiency in mathematics
The outcomes of the PISA mathematics assessment are reported in a number of ways. Estimates of overall mathematical proficiency are obtained for sampled students in each participating country, and a number of proficiency levels are defined. Descriptions of the degree of mathematical literacy typical of students in each level are also developed. For PISA 2003, scales based on the four broad content categories were developed. In Table 3.5, descriptions of the six proficiency levels reported for the overall PISA mathematics scale in 2012 are presented. These form the basis of the PISA 2018 mathematics scale. The finalised 2012 scale is used to report the PISA 2018 outcomes. As mathematical literacy is a minor domain in 2018, only the overall proficiency scale is reported.
Fundamental mathematical capabilities play a central role in defining what it means to be at different levels of the scales for mathematical literacy overall and for each of the reported processes. For example, in the proficiency scale description for Level 4 (see Table 3.5), the second sentence highlights aspects of mathematising and representation that are evident at this level. The final sentence highlights the characteristic communication, reasoning and argument of Level 4, providing a contrast with the short communications and lack of argument of Level 3 and the additional reflection of Level 5. In an earlier section of this framework and in Table 3.2, each of the mathematical processes was described in terms of the fundamental mathematical capabilities that individuals might activate when engaging in that process.
References
[17] Bennett, R. (2003), Online Assessment and the Comparability of Score Meaning, Educational Testing Service, Princeton, NJ.
[15] Bennett, R. et al. (2008), “Does it Matter if I Take My Mathematics Test on Computer? A Second Empirical Study of Mode Effects in NAEP”, The Journal of Technology, Learning, and Assessment, Vol. 6/9, http://www.jtla.org.
[3] Blum, W., P. Galbraith and M. Niss (2007), “Introduction”, in Blum, W. et al. (eds.), Modelling and Applications in Mathematics Education, Springer US, New York, https://doi.org/10.1007/978-0-387-29822-1.
[5] Gagatsis, A. and S. Papastavridis (eds.) (2003), Mathematical Competencies and the Learning of Mathematics: The Danish KOM Project, Hellenic Mathematic Society, Athens.
[12] Hoyles, C. et al. (2002), “Mathematical Skills in the Workplace: Final Report to the Science Technology and Mathematics Council”, Institute of Education, University of London; Science, Technology and Mathematics Council, London. (2002), http://discovery.ucl.ac.uk/1515581/ (accessed on 5 April 2018).
[16] Mason, B., M. Patry and D. Bernstein (2001), “An Examination of the Equivalence Between Non-Adaptive Computer-Based And Traditional Testing”, Journal of Education Computing Research, Vol. 24/1, pp. 29-39.
[10] Moore, D. (1997), “New Pedagogy and New Content: The Case of Statistics”, International Statistical Review, Vol. 65/2, pp. 123-165, https://onlinelibrary.wiley.com/doi/epdf/10.1111/j.1751-5823.1997.tb00390.x.
[7] Niss, M. and T. Højgaard (2011), Competencies and Mathematical Learning: Ideas and Inspiration for the Development of Mathematics Teaching and Learning in Denmark, Ministry of Education, Roskilde University, https://pure.au.dk/portal/files/41669781/thj11_mn_kom_in_english.pdf.
[6] Niss, M. and T. Jensen (2002), Kompetencer og matematiklaering Ideer og inspiration til udvikling af matematikundervisning i Danmark, Ministry of Education, Copenhagen, http://static.uvm.dk/Publikationer/2002/kom/hel.pdf.
[20] OECD (2016), PISA 2015 Results (Volume I): Excellence and Equity in Education, OECD Publishing, Paris, https://doi.org/10.1787/19963777.
[19] OECD (2014), Technical Report of the Survey of Adult Skills (PIAAC) 2013, Pre-publication, OECD, http://www.oecd.org/skills/piaac/_Technical%20Report_17OCT13.pdf.
[4] OECD (2013), PISA 2012 Assessment and Analytical Framework: Mathematics, Reading, Science, Problem Solving and Financial Literacy, PISA, OECD Publishing, Paris, https://doi.org/10.1787/9789264190511-en.
[1] OECD (2010), Pathways to Success: How Knowledge and Skills at Age 15 Shape Future Lives in Canada, PISA, OECD Publishing, Paris, https://dx.doi.org/10.1787/9789264081925-en.
[2] OECD (2004), The PISA 2003 Assessment Framework: Mathematics, Reading, Science and Problem Solving Knowledge and Skills, PISA, OECD Publishing, Paris, https://doi.org/10.1787/9789264101739-en.
[13] Richardson, M. et al. (2002), “Challenging minds? Students’ perceptions of computer-based World Class Tests of problem solving”, Computers in Human Behavior, Vol. 18/6, pp. 633-649, https://doi.org/10.1016/S0747-5632(02)00021-3.
[14] Sandene, B. et al. (2005), Online Assessment in Mathematics and Writing: Reports from the NAEP Technology-Based Assessment Project, Research and Development Series (NCES 2005-457), US Department of Education, National Center for Education Statistics, US Government Printing Office.
[9] Turner, R. and R. Adams (2012), Some Drivers of Test Item Difficulty in Mathematics: An Analysis of the Competency Rubric, American Educational Research Association (AERA), http://research.acer.edu.au/pisa.
[8] Turner, R. et al. (2013), “Using mathematical competencies to predict item difficulty in PISA”, in Research on PISA. Research outcomes of the PISA research conference 2009, Kiel, Germany, September 14–16, 2009, Springer, New York, https://doi.org/10.1007/978-94-007-4458-5_2.
[18] Wang, S. et al. (2007), “A meta-analysis of testing mode effects in grade K-12 mathematics tests”, Educational and Psychological Measurement, Vol. 67/2, pp. 219-238, https://doi.org/10.1177/0013164406288166.
[11] Watson, J. and R. Callingham (2003), “Statistical Literacy: A Complex Hierarchical Construct”, Statistics Education Research Journal, Vol. 2/2, pp. 3-46, http://fehps.une.edu.au/serj.
Note
← 1. In some countries, “mathematical tools” can also refer to established mathematical procedures, such as algorithms. For the purposes of the PISA framework, “mathematical tools” refers only to the physical and digital tools described in this section.